ЬтФПФкШн
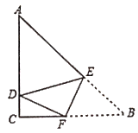
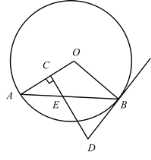
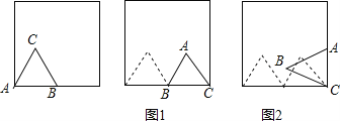
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ1ЕФе§Ш§НЧаЮABCЗХжУдкБпГЄЮЊ2ЕФе§ЗНаЮФкВПЃЌЖЅЕуAдке§ЗНаЮЕФвЛИіЖЅЕуЩЯЃЌБпABдке§ЗНаЮЕФвЛБпЩЯЃЌНЋЁїABCШЦЕуBЫГЪБеыа§зЊЃЌЕБЕуCТфдке§ЗНаЮЕФБпЩЯЪБЃЌЭъГЩЕк1ДЮЮоЛЌЖЏЙіЖЏЃЈШчЭМ1ЃЉЃЛдйНЋЁїABCШЦЕуCЫГЪБеыа§зЊЃЌЕБЕуAТфдке§ЗНаЮЕФБпЩЯЪБЃЌЭъГЩЕк2ДЮЮоЛЌЖЏЙіЖЏЃЈШчЭМ2ЃЉЃЌЁЃЌУПДЮа§зЊЕФНЧЖШЖМВЛДѓгк120ЁуЃЌвРДЮетбљВйзїЯТШЅЃЌЕБЭъГЩЕк2016ДЮЮоЛЌЖЏЙіЖЏЪБЃЌЕуAОЙ§ЕФТЗОЖзмГЄЮЊ ______ЃЎ
ЁОД№АИЁП560ІаЃЎ
ЁОНтЮіЁП
ЯШЧѓГіЕквЛДЮЕНЕкСљДЮа§зЊЕФТЗОЖЕФГЄЗжБ№ЪЧЖрЩйЃЌЬНОПЙцТЩКѓМДПЩНтОіЮЪЬтЃЎ
ЕквЛДЮа§зЊЕФТЗОЖГЄЮЊ![]() =
=![]() ІаЃЌ
ІаЃЌ
ЕкЖўДЮа§зЊЕФТЗОЖГЄЮЊ![]() =
=![]() ІаЃЌ
ІаЃЌ
ЕкШ§ДЮа§зЊЕФТЗОЖГЄЮЊ0ЃЌ
ЕкЫФДЮа§зЊЕФТЗОЖГЄЮЊ![]() ІаЃЌ
ІаЃЌ
ЕкЮхДЮа§зЊЕФТЗОЖГЄЮЊ![]() ІаЃЌ
ІаЃЌ
ЕкСљДЮа§зЊЕФТЗОЖГЄЮЊ0ЃЌ
Ё
гЩДЫЗЂЯжУПШ§ДЮа§зЊЕФТЗОЖКЭЮЊ![]() Іа+
Іа+![]() Іа=
Іа=![]() ІаЃЎ
ІаЃЎ
2016ЁТ3=672ЃЌ
ЁрЭъГЩЕк2016ДЮЮоЛЌЖЏЙіЖЏЪБЃЌЕуAОЙ§ЕФТЗОЖзмГЄЮЊ672ЁС![]() Іа=560ІаЃЎ
Іа=560ІаЃЎ
ЙЪД№АИЮЊ560ІаЃЎ