题目内容
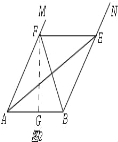
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 、
、![]() 上的点,沿直线
上的点,沿直线![]() 将
将![]() 折叠,使点B恰好落在
折叠,使点B恰好落在![]() 上的
上的![]() 处,当
处,当![]() 恰好为直角三角形时,
恰好为直角三角形时,![]() 的长为__________.
的长为__________.
【答案】![]() 或
或![]()
【解析】
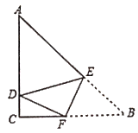
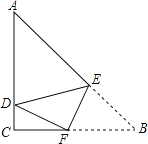
先在Rt△ABC中利用勾股定理求出AC=6cm,再根据折叠的性质得到BE=DE,直线EF将∠B折叠,使点B恰好落在BC上的D处,△ADE恰好为直角三角形,有两种可能:①∠ADE=90°,②∠AED=90°,设BE=x,运用三角形相似列比例式解方程即可得解.
解:在Rt△ABC中,∵∠C=90°,AB=5,AC=4,
∴BC=3.
直线EF将∠B折叠,使点B恰好落在BC上的D处,当△ADE恰好为直角三角形时,
根据折叠的性质:BE=DE
设BE=x,则DE=x,AE=10-x
①当∠ADE=90°时,则DE∥BC,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
②当∠AED=90°时,
则△AED∽△ACB,
∴![]() ,
,
∴![]() ,
,
解得:x=![]() ,
,
故所求BE的长度为:![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目