题目内容
【题目】已知△ABC是等边三角形，点P是平面内一点，且四边形PBCD为平行四边形，将线段CD绕点C逆时针旋转60°，得到线段CF
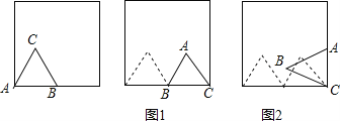
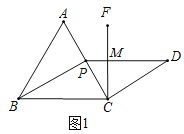
(1)如图1，当P为AC的中点时，求证：FC⊥PD.
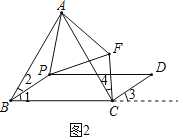
(2)如图2，当P为△ABC内任一点时，连接PA、PF、AF，试判断△PAF的形状，并证明你的结论.
(3)当B、P、F三点共线且AB=
，PB=3时，求PA的长.
【答案】（1）见解析；（2）△PAF是等边三角形，证明见解析；（3）PA的长为2或5．
【解析】
（1）如图1，利用等边三角形和平行四边形的性质求得∠FCD+∠D＝90°即得结论；
（2）△PAF是等边三角形．如图2，延长BC，先利用等边三角形的性质和平行四边形的性质证得∠2＝∠4，再根据SAS证明△ABP≌△ACF，进一步根据等边三角形的判定定理即可证得结论；
（3）需要分类讨论：当点P在线段BF上和当点P落在线段FB的延长线上两种情况，通过作辅助线，构造直角三角形，再结合勾股定理即可求出结果．
（1）证明：如图1，设FC、PD交于点M，
∵△ABC是等边三角形，P为AC的中点，
∴∠PBC＝
∠ABC＝×60°＝30°，
∵四边形PBCD为平行四边形，
∴∠D＝∠PBC＝30°．
∵∠FCD＝60°，
∴∠FCD+∠D＝90°，
∴∠CMD＝90°，
∴FC⊥PD；
（2）△PAF是等边三角形，理由如下：
如图2，延长BC，∵△ABC为等边三角形，
∴AB＝AC，∠ABC＝∠ACB＝60°，
∴∠2＝60°﹣∠1，∠4＝180°﹣60°﹣60°﹣∠3＝60°﹣∠3．
∵四边形PBCD是平行四边形，
∴PB∥CD，PB＝CD＝FC．
∴∠1＝∠3，∴∠2＝∠4．
又AB＝AC，PB＝FC，
∴△ABP≌△ACF（SAS）．
∴AP＝AF，∠BAP＝∠CAF．
∵∠BAP+∠PAC＝60°，
∴∠PAC+∠CAF＝∠PAF＝60°，
∴△PAF是等边三角形；
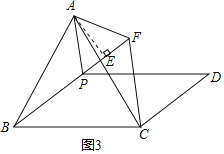
（3）①当点P在线段BF上时，如图3，过A作AE⊥BF于E，由（2）可得∠APF＝60°，
设PE＝x，则AE＝
x，
于是在Rt△ABE中，根据勾股定理得：
，
解得：x1＝1，x2＝
（不合题意，舍去）
∴PA＝2x＝2；
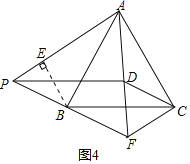
②当点P落在线段FB的延长线上时，如图4，过B作BE⊥PA于E，
则在Rt△PBE中，PB＝3，由（2）可得∠BPE＝60°，∴∠PBE＝30°．
∴PE＝
，BE＝
．
在Rt△ABE中，AB＝
，BE＝，∴AE＝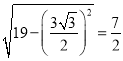
，
∴PA＝PE+AE＝5．
由于P点不可能在线段BF的延长线上，所以， PA的长为2或5．
