题目内容
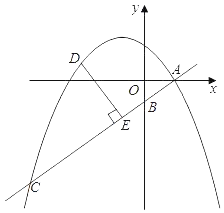
【题目】如图,![]() 是
是![]() 的弦,过
的弦,过![]() 的中点
的中点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
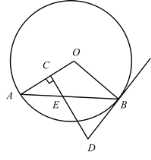
【答案】(1)见解析;(2)204
【解析】
(1)要证明DB=DE,只要证明∠DEB=∠DBE即可;
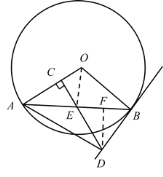
(2)作DF⊥AB于F,连接OE.只要证明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE=![]() ,由此求出AO的长,由勾股定理可求OE的长即可解决问题.
,由此求出AO的长,由勾股定理可求OE的长即可解决问题.
证明:(1)∵AO=OB,
∴∠OAB=∠OBA,
∵BD是切线,
∴OB⊥BD,
∴∠OBD=90°,
∴∠OBE+∠EBD=90°,
∵EC⊥OA,
∴∠CAE+∠CEA=90°,
∵∠CEA=∠DEB,
∴∠EBD=∠BED,
∴DB=DE.
(2)作DF⊥AB于F,连接OE.
∵DB=DE,AE=EB=![]() AB=12,
AB=12,
∴EF=![]() BE=6,OE⊥AB,
BE=6,OE⊥AB,
在Rt△EDF中,DE=BD=10,EF=6,
∴DF=![]() ,
,
∵∠AOE+∠OAB=90°,∠DEF+∠OAB=90°,
∴∠AOE=∠DEF,
∴sin∠DEF=sin∠AOE=![]() ,
,
∵AE=12,
∴AO=15
∴OE=![]()
∴四边形OADB的面积=![]() ×AB×OE+
×AB×OE+![]() ×AB×DF=204.
×AB×DF=204.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目