题目内容
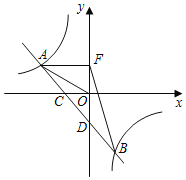
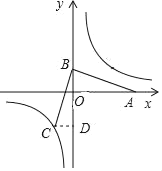
【题目】在平面直角坐标系中，点A的坐标为（4，0），点B为y轴上的一动点，将线段AB绕点B顺时针旋转90°得线段BC，若点C恰好落在反比例函数y＝
的图象上，则点B的坐标为_____．
【答案】（0，1）或（0，3）
【解析】
设B（0，n），根据旋转的性质可以得到CD＝OB＝n，BD＝OA＝4，得到点C的坐标是（﹣n，n﹣4），即可得到﹣n（n﹣4）＝3，从而求得点B的坐标．
解：设B（0，n），
∵点A的坐标为（4，0），将线段AB绕点B顺时针旋转90°得线段BC，若点C恰好落在反比例函数y＝
的图象上，
易证△AOB≌△BDC，
设B（0，n），
∴CD＝OB＝n，BD＝OA＝4，
∴点C的坐标是（﹣n，n﹣4），
∵C恰好落在反比例函数y＝的图象上，
∴﹣n（n﹣4）＝3，
解得n＝1，3，
∴点B的坐标是（0，1）或（0，3），
故答案为（0，1）或（0，3）．
练习册系列答案
相关题目
