题目内容
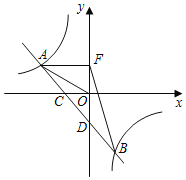
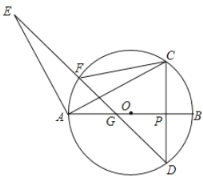
【题目】 如图,平面直角坐标系中,矩形OABC的顶点B的坐标为(7,5),顶点A,C分别在x轴,y轴上,点D的坐标为(0,1),过点D的直线与矩形OABC的边BC交于点G,且点G不与点C重合,以DG为一边作菱形DEFG,点E在矩形OABC的边OA上,设直线DG的函数表达式为y=kx+b
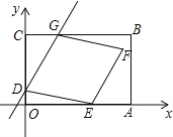
(1)当CG=OD时,求直线DG的函数表达式;
(2)当点E的坐标为(5,0)时,求直线DG的函数表达式;
(3)连接BF,设△FBG的面积为S,CG的长为a,请直接写出S与a的函数表达式及自变量a的取值范围.
【答案】(1)y=4x+1;(2)y=![]() x+1;(3)S=
x+1;(3)S=![]() (7-a)(0<a≤
(7-a)(0<a≤![]() )
)
【解析】
(1)利用矩形的性质结合点B的坐标可得出点A,C的坐标,由点D的坐标结合CG=OD可得出点G的坐标,由点D,G的坐标,利用待定系数法即可求出直线DG的函数表达式;
(2)利用勾股定理可求出DE的长,由菱形的性质及勾股定理可求出CG的长,进而可得出点G的坐标,由点D,G的坐标,利用待定系数法即可求出直线DG的函数表达式;
(3)设DG交x轴于点P,过点F作FM⊥x轴于点M,延长MF交BC于点N,易证△DCG≌△FME(AAS),利用全等三角形的性质可得出FM的长度,进而可得出FN的长,再利用三角形的面积公式可得出S与a的函数表达式,结合点G不与点C重合及点E在OA上可求出a的取值范围,此题得解.
解:(1)∵四边形OABC为矩形,点B的坐标为(7,5),点A,C分别在x轴,y轴上,
∴点C的坐标为(0,5),点A的坐标为(7,0).
∵点D的坐标为(0,1),CG=OD,
∴点G的坐标为(1,5).
将D(0,1),G(1,5)代入y=kx+b,得:
![]() ,
,
解得:![]() ,
,
∴当CG=OD时,直线DG的函数表达式为y=4x+1.
(2)在Rt△ODE中,OD=1,OE=5,∠DOE=90°,
∴DE=![]() =
=![]() .
.
∵四边形DEFG为菱形,
∴DG=DE=![]() .
.
在Rt△CDG中,DG=![]() ,CD=OC-OD=4,∠DCG=90°,
,CD=OC-OD=4,∠DCG=90°,
∴CG=![]() =
=![]() ,
,
∴点G的坐标为(![]() ,5).
,5).
将D(0,1),G(![]() ,5)代入y=kx+b,得:
,5)代入y=kx+b,得:
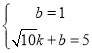 ,
,
解得: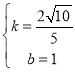 ,
,
∴当CG=OD时,直线DG的函数表达式为y=![]() x+1.
x+1.
(3)设DG交x轴于点P,过点F作FM⊥x轴于点M,延长MF交BC于点N,如图所示.
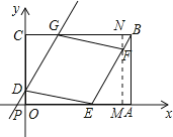
∵DG∥EF,
∴∠FEM=∠GPO.
∵BC∥OA,
∴∠DGC=∠GPO=∠FEM.
在△DCG和△FME中,
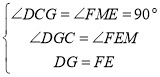 ,
,
∴△DCG≌△FME(AAS),
∴FM=DC=4.
∵MN⊥x轴,
∴四边形OMNC为矩形,
∴MN=OC=5,FN=MN-FM=1.
∵CG的长为a,
∴BG=BC-CG=7-a
∴S=![]() BGFN=
BGFN=![]() (7-a).
(7-a).
∵点E在边OA上,点G在BC边上,且点G不与点C重合,
∴DE≤![]() =5
=5![]() ,a>0,
,a>0,
∴DG=![]() ≤5
≤5![]() ,
,
∴0<a≤![]() .
.
∴S与a的函数表达式为S=![]() (7-a)(0<a≤
(7-a)(0<a≤![]() ).
).

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案