题目内容
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点( ![]() ,
, ![]() )的“双角坐标”为;
)的“双角坐标”为;
(2)若点P到x轴的距离为 ![]() ,则m+n的最小值为 .
,则m+n的最小值为 .
【答案】
(1)(60°,60°)
(2)90
【解析】解:(1)∵P( ![]() ,
, ![]() ),OA=1, ∴tan∠POA=
),OA=1, ∴tan∠POA= ![]() =
= ![]() ,tan∠PAO=
,tan∠PAO= ![]() =
= ![]() ,
,
∴∠POA=60°,∠PAO=60°,
即点P的“双角坐标”为(60°,60°),
故答案为:(60°,60°);
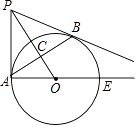
⑵根据三角形内角和定理知若要使m+n取得最小值,即∠POA+∠PAO取得最小值,则∠OPA需取得最大值,如图,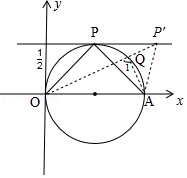
∵点P到x轴的距离为 ![]() ,OA=1,
,OA=1,
∴OA中点为圆心, ![]() 为半径画圆,与直线y=
为半径画圆,与直线y= ![]() 相切于点P,
相切于点P,
在直线y= ![]() 上任取一点P′,连接P′O、P′A,P′O交圆于点Q,
上任取一点P′,连接P′O、P′A,P′O交圆于点Q,
∵∠OPA=∠1>∠OP′A,
此时∠OPA最大,∠OPA=90°,
∴m+n的最小值为90,
故答案为:90.
(1)分别求出tan∠POA、tan∠PAO即可得∠POA、∠PAO的度数,从而得出答案;(2)根据三角形内角和定理知若要使m+n取得最小值,即∠POA+∠PAO取得最小值,则∠OPA需取得最大值,OA中点为圆心, ![]() 为半径画圆,与直线y=
为半径画圆,与直线y= ![]() 相切于点P,由∠OPA=∠1>∠OP′A知此时∠OPA最大,∠OPA=90°,即可得出答案.
相切于点P,由∠OPA=∠1>∠OP′A知此时∠OPA最大,∠OPA=90°,即可得出答案.

练习册系列答案
相关题目