题目内容
【题目】在图1﹣﹣图4中，菱形ABCD的边长为3，∠A=60°，点M是AD边上一点，且DM= 
AD，点N是折线AB﹣BC上的一个动点．
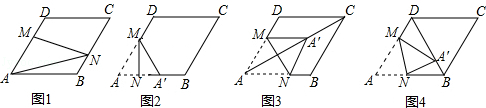
（1）如图1，当N在BC边上，且MN过对角线AC与BD的交点时，则线段AN的长度为 ．
（2）当点N在AB边上时，将△AMN沿MN翻折得到
△A′MN，如图2，
①若点A′落在AB边上，则线段AN的长度为 
；
②当点A′落在对角线AC上时，如图3，求证：四边形AM A′N是菱形；
③当点A′落在对角线BD上时，如图4，求 
的值．
【答案】
（1）
（2）
①1
②在菱形ABCD中，∠A=60°，
∴∠DAC=∠BAC=30°，
∵点A′落在对角线AC上，
∴MN⊥AC，
∴∠AMN=∠ANM=60°，
∴AM=AN，
由折叠的性质可知，AM=AN=A′M=A′N，
∴四边形AM A′N是菱形；
③∠A′=∠A=60°，
∴∠BA′N+∠DA′M=120°，又∠DMA′+∠DA′M=120°，
∴∠BA′N=∠DMA′，又∠A′DM=∠NBA′，
∴△A′DM∽△NBA′，
∴ 
= 
= 
=2．
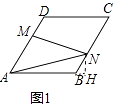
【解析】解：（1）作NH⊥AB交AB的延长线于H，
∵AD=3，
∴DM= 
AD=1，AM=2，
∵菱形的中心对称图形，MN过对角线AC与BD的交点，
∴BN=DM=1，
∵∠DAB=60°，
∴∠NBH=60°，
∴BH= 
BN= ，NH= 
BN= ，
∴AN= 
= ，
故答案为： ；
⑵①∵点A′落在AB边上，
∴MN⊥AA′，
∴AN= AM=1，
故答案为：1；
（1）作NH⊥AB交AB的延长线于H，根据题意求出DM、AM，根据菱形的中心对称图形得到BN=DM=1，根据直角三角形的性质求出BH、NH，根据勾股定理计算；（2）①根据直角三角形的性质计算；②根据翻转变换的性质、菱形的判定定理进行证明；③证明△A′DM∽△NBA′，根据相似三角形的性质计算即可．
