Question

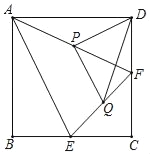
【题目】如图，正方形ABCD中，点E、F分别是BC、CD上的点，且CE=CF，点P、Q分别是AF、EF的中点，连接PD、PQ、DQ，则△PQD的形状是（　　）

A. 等腰三角形 B. 直角三角形

C. 等腰非直角三角形 D. 等腰直角三角形

Answer 1

【答案】D

【解析】

可证ΔADF≌ΔABE,可得AF=AE,由点P、Q分别是AF、EF的中点，可得PD=PQ=,可证∠DPQ为直角，可得答案.

解：有题意得，正方形ABCD中，CE=CF，DF=BE,

在RTΔADF与RTΔABE中有 ，DF=BE，AD=AB,

故ΔADF≌ΔABE，AF=AE，∠DAF=∠BAE

又AP=DP, ∠DAF=∠BAE=∠ADP.

点P、Q分别是AF、EF的中点，PD=PQ=，

PQ∥AE,∠FPQ=∠FAE,

∠DPQ=∠FPQ+∠DPF=∠FAE+ ∠DAF+∠ADP.= ∠FAE+ ∠DAF+∠BAE=，

△PQD为等腰直角三角形，

故选D.