题目内容
【题目】先阅读所给材料再完成后面的问题:
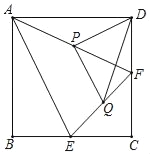
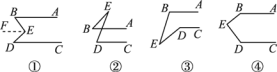
如图①所示,AB∥CD,试说明∠B+∠D=∠BED.
解:过点E作EF∥CD,易知EF∥AB,所以∠DEF=∠D,∠FEB=∠B,所以∠BED=∠FEB+∠DEF=∠B+∠D.若图中点E的位置发生变化,如图②③④所示,则上面问题中的三个角(均小于180°)有何数量关系?写出结论,并选择图②说明理由.
【答案】见解析
【解析】
根据题意构造平行线,运用平行线的性质进行推理.
图②中,∠BED+∠B=∠D.理由如下:
过点E作EF∥AB,如图所示.
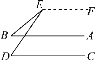
易知∠BEF+∠B=180°.①
又因为AB∥CD,所以EF∥CD,所以∠DEF+∠D=180°.②
①-②,得∠BEF+∠B-∠DEF-∠D=180°-180°,
所以∠BED+∠B=∠D.
图③中,∠D-∠B=∠BED.图④中,∠BED+∠B+∠D=360°.

【题目】“十一”黄金周期间,深圳世界之窗风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | ﹣0.4 | ﹣0.8 | +0.2 | ﹣1.2 |
(1)请判断七天内游客人数最多的是 日,最少的是 日.
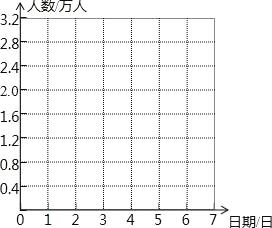
(2)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数的变化情况.
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.