题目内容
【题目】如图,抛物线y=﹣x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B.过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.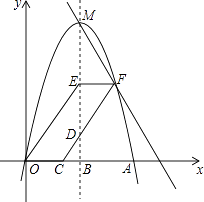
(1)求点A,M的坐标.
(2)当BD为何值时,点F恰好落在该抛物线上?
(3)当BD=1时
求直线MF的解析式,并判断点A是否落在该直线上.
(4)②延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1 , S2 , S3 , 则S1:S2:S3= .
【答案】
(1)
解:令y=0,则﹣x2+6x=0,解得x=0或x=6,
∴A点坐标为(6,0),
又∵y=﹣x2+6x=﹣(x﹣3)2+9,
∴M点坐标为(3,9)
(2)
解:∵OE∥CF,OC∥EF,
∴四边形OCFE为平行四边形,且C(2,0),
∴EF=OC=2,
又B(3,0),
∴OB=3,BC=1,
∴F点的横坐标为5,
∵点F落在抛物线y=﹣x2+6x上,
∴F点的坐标为(5,5),
∴BE=5,
∵OE∥CF,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴BD= ![]() ;
;
(3)
解:当BD=1时,由(2)可知BE=3BD=3,
∴F(5,3),
设直线MF解析式为y=kx+b,
把M、F两点坐标代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直线MF解析式为y=﹣3x+18,
∵当x=6时,y=﹣3×6+18=0,
∴点A落在直线MF上
(4)3:4:8
【解析】解:(4)如图所示,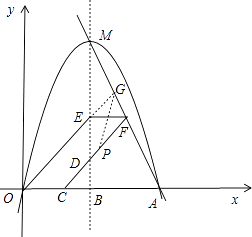
∵E(3,3),
∴直线OE解析式为y=x,
联立直线OE和直线MF解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴G( ![]() ,
, ![]() ),
),
∴OG= ![]() =
= ![]() ,OE=CF=3
,OE=CF=3 ![]() ,
,
∴EG=OG﹣OE= ![]() ﹣3
﹣3 ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴CD= ![]() OE=
OE= ![]() ,
,
∵P为CF中点,
∴PF= ![]() CF=
CF= ![]() ,
,
∴DP=CF﹣CD﹣PF=3 ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∵OG∥CF,
∴可设OG和CF之间的距离为h,
∴S△FPG= ![]() PFh=
PFh= ![]() ×
× ![]() h=
h= ![]() h,
h,
S四边形DEGP= ![]() (EG+DP)h=
(EG+DP)h= ![]() ×(
×( ![]() +
+ ![]() )h=
)h= ![]() h,
h,
S四边形OCDE= ![]() (OE+CD)h=
(OE+CD)h= ![]() (3
(3 ![]() +
+ ![]() )h=2
)h=2 ![]() h,
h,
∴S1 , S2 , S3= ![]() h:
h: ![]() h:2
h:2 ![]() h=3:4:8,
h=3:4:8,
所以答案是:3:4:8.

【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).





