Question

【题目】图甲是小明设计的带菱形图案的花边作品．该作品由形如图乙的矩形图案拼接而成（不重叠、无缝隙）．图乙中 ，EF=4cm，上下两个阴影三角形的面积之和为54cm2 ， 其内部菱形由两组距离相等的平行线交叉得到，则该菱形的周长为cm．

Answer 1

【答案】
【解析】解：如图乙，H是CF与DN的交点，取CD的中点G，连接HG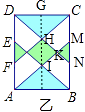， ， 设AB=6acm，则BC=7acm，中间菱形的对角线HI的长度为xcm，
∵BC=7acm，MN=EF=4cm，
∴CN= ，
∵GH∥BC，
∴ ，
∴ ，
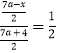∴x=3.5a﹣2…（1）；
∵上下两个阴影三角形的面积之和为54cm2 ，
∴6a（7a﹣x）÷2=54，
∴a（7a﹣x）=18…（2）；
由（1）（2），可得
a=2，x=5，
∴CD=6×2=12（cm），CN= ，
∴DN= =15（cm），
又∵DH= = =7.5（cm），
∴HN=15﹣7.5=7.5（cm），
∵AM∥FC，
∴ = ，
∴HK= ，
∴该菱形的周长为：
= （cm）．
所以答案是： ．
【考点精析】认真审题，首先需要了解菱形的性质(菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半)，还要掌握矩形的性质(矩形的四个角都是直角，矩形的对角线相等)的相关知识才是答题的关键．