题目内容
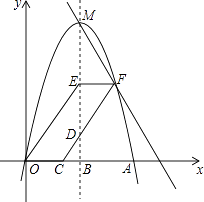
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα= ![]() .
. 
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55cm,求铁环钩MF的长度.
【答案】
(1)解:过点M作MD⊥OA交OA于点D,
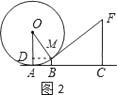
在RT△ODM中,sinα= ![]() ,
,
∴DM=15cm∴OD=20 cm,
∴AD=BM=5cm
(2)解:延长DM交CF于点E,
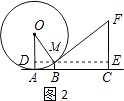
易得:∠FME=∠AOM=α,
∵ME=AC﹣DM=55﹣15=40cm,
∴cosα= ![]()
∴MF=50cm.
【解析】(1)过M作与AC平行的直线,与OA、FC分别相交于H、N.那么求BM的长就转化为求HA的长,而要求出HA,必须先求出OH,在直角三角形OHM中,sinα的值,且铁环的半径为5个单位即OM=5,可求得HM的值,从而求得HA的值;(2)因为∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,又因为sin∠MOA= ![]() ,所以可得出FN和FM之间的数量关系,即FN=
,所以可得出FN和FM之间的数量关系,即FN= ![]() FM,再根据MN=11﹣3=8,利用勾股定理即可求出FM=10个单位.
FM,再根据MN=11﹣3=8,利用勾股定理即可求出FM=10个单位.

【题目】为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
组别 | 成绩x(分) | 频数(人数) |
A | 8.0≤x<8.5 | a |
B | 8.5≤x<9.0 | 8 |
C | 9.0≤x<9.5 | 15 |
D | 9.5≤x<10 | 3 |

(1)图中a= , 这次比赛成绩的众数落在组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
【题目】如图,点A在双曲线y= ![]() 的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .
的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .