题目内容
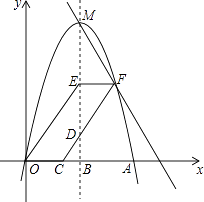
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 ![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
【答案】
(1)
解:∵y=﹣x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=3,即A点坐标为(3,0),当x=0时,y=3,即B点坐标为(0,3).
∵将A(3,0),B(0,3)代入得: ![]() ,
,
解得 ![]() .
.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)
解:∵OA=OB=3,∠BOA=90°,
∴∠QAP=45°.
如图①所示:∠PQA=90°时.
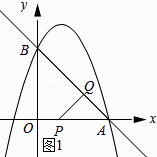
设运动时间为t秒,则QA= ![]() t,PA=3﹣t.
t,PA=3﹣t.
在Rt△PQA中, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t=1.
如图②所示:∠QPA=90°时.
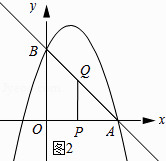
设运动时间为t秒,则QA= ![]() t,PA=3﹣t.
t,PA=3﹣t.
在Rt△PQA中, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() .
.
综上所述,当t=1或t= ![]() 时,△PQA是直角三角形.
时,△PQA是直角三角形.
(3)
解:如图③所示:
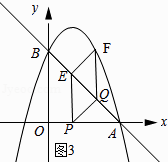
设点P的坐标为(t,0),则点E的坐标为(t,﹣t+3),
则EP=3﹣t.点Q的坐标为(3﹣t,t),点F的坐标为(3﹣t,﹣(3﹣t)2+2(3﹣t)+3),即F(3﹣t,4t﹣t2),
则FQ=4t﹣t2﹣t=3t﹣t2.
∵EP∥FQ,EF∥PQ,
∴四边形EFQP为平行四边形.
∴EP=FQ,即3﹣t=3t﹣t2.
解得:t1=1,t2=3(舍去).
将t=1代入得点F的坐标为(2,3).
【解析】(1)先求得直线AB与x轴、y轴的交点坐标,然后将点A、点B的坐标代入抛物线的解析式得到关于b、c的方程组求得b、c的值从而可得到抛物线的解析式;(2)由点A、B的坐标可知OB=OA,从而可求得∠BAO=45°,然后分为∠PQA=90°和∠QPA=90°两种情况求解即可;(3)由题意可知:EP∥FQ,EF∥PQ,故此四边形EFQP为平行四边形,从而得到PE=FQ,然后设点P的坐标为(t,0)则可表示出点Q、E、F的坐标,从而可求得PE、FQ的长,最后根据PE=FQ列方程求解即可.

【题目】为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
组别 | 成绩x(分) | 频数(人数) |
A | 8.0≤x<8.5 | a |
B | 8.5≤x<9.0 | 8 |
C | 9.0≤x<9.5 | 15 |
D | 9.5≤x<10 | 3 |

(1)图中a= , 这次比赛成绩的众数落在组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.