题目内容
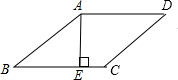
如图，在菱形ABCD中，AE⊥BC于E点，EC=1，sinB=
，求四边形AECD的周长．
| 5 |
| 13 |
在菱形ABCD中，AB=BC=CD=DA
∵AE⊥BC
∴∠AEB=90°
在直角三角形ABE中，sinB=
又sinB=
设AE=5x（x＞0），则AB=13x
根据勾股定理，得
BE=
=12x
∵BE+EC=BC，EC=1
∴12x+1=13x
解得x=1
∴AB=DA=CD=13，AE=5
∴AE+EC+CD+DA=5+1+13+13=32．
即四边形AECD的周长是32．
∵AE⊥BC
∴∠AEB=90°
在直角三角形ABE中，sinB=
| AE |
| AB |
又sinB=
| 5 |
| 13 |
设AE=5x（x＞0），则AB=13x
根据勾股定理，得
BE=
| AB2-AE2 |
∵BE+EC=BC，EC=1
∴12x+1=13x
解得x=1
∴AB=DA=CD=13，AE=5
∴AE+EC+CD+DA=5+1+13+13=32．
即四边形AECD的周长是32．
练习册系列答案
阅读快车系列答案
相关题目
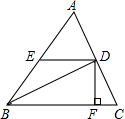BC，交AB于E，过D作DF⊥BC，垂足为F，连接BD，设CD=x．
