Question

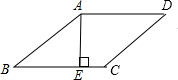
如图，在△ABC中，AC=15，BC=18，sinC=

4

5

，D是AC上一个动点（不运动至点A，C），过D作DE∥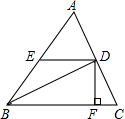BC，交AB于E，过D作DF⊥BC，垂足为F，连接BD，设CD=x．
（1）用含x的代数式分别表示DF和BF；
（2）如果梯形EBFD的面积为S，求S关于x的函数关系式；
（3）如果△BDF的面积为S₁，△BDE的面积为S₂，那么x为何值时，S₁=2S₂．

Answer 1

（1）在Rt△CDF中，sinC=

4

5

，CD=x
∴DF=CD•sinC=

4

5

x，CF=

CD2-DF2

=

3

5

x
∴BF=18-

3

5

x；

（2）∵ED∥BC，
∴

ED

BC

=

AD

AC

．
∴ED=

BC•AD

AC

=

18×(15-x)

15

=18-

6

5

x．
∴S=

1

2

×DF×（ED+BF）
=

1

2

×

4

5

x×（18-

6

5

x+18-

3

5

x）=-

18

25

x²+

72

5

x；

（3）由S₁=2S₂，得S₁=

2

3

S，
∴

1

2

（18-

3

5

x）•

4

5

x=

2

3

（-

18

25

x²+

72

5

x），
解得：x=10
所以，当x=10时，S₁=2S₂．