题目内容
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 和
和![]() 的顶点坐标分别为
的顶点坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
按下列要求画图:以点![]() 为位似中心,将
为位似中心,将![]() 向
向![]() 轴左侧按比例尺
轴左侧按比例尺![]() 放大得
放大得![]() 的位似图形
的位似图形![]() ,并解决下列问题:
,并解决下列问题:
(1)顶点![]() 的坐标为 ,
的坐标为 , ![]() 的坐标为 ,
的坐标为 , ![]() 的坐标为 ;
的坐标为 ;
(2)请你利用旋转、平移两种变换,使![]() 通过变换后得到
通过变换后得到![]() ,且
,且![]() 恰与
恰与![]() 拼接成一个平行四边形 (非正方形).写出符合要求的变换过程.
拼接成一个平行四边形 (非正方形).写出符合要求的变换过程.
【答案】见解析
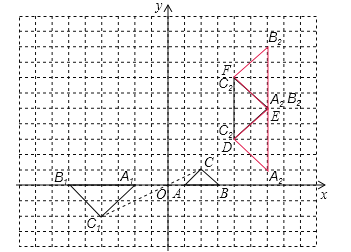
【解析】试题分析:(1)延长AO到A1,使A1O=2AO,延长BO到B1,使B1O=2BO,连接CO并延长到C1,使C1O=2CO,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标即可;
(2)先绕点O顺时针旋转90°,然后向右平移再向下(或向上)平移,使△A2B2C2的直角边与△DEF的直角边重合即可.
试题解析:解:(1)如图所示,△A1B1C1即为所求作的三角形,A1(﹣2,0)B1(﹣6,0)C1(﹣4,﹣2);
(2)如图,把△A1B1C1绕点O顺时针旋转90°,再向右平移6个单位,向下平移1个单位,使B2C2与DE重合,或者:把△A1B1C1绕点O顺时针旋转90°,再向右平移6个单位,向上平移3个单位,使A2C2与EF重合,都可以拼成一个平行四边形.

练习册系列答案
相关题目


