题目内容
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
【答案】(1)![]() ;(2)不公平,理由见解析.
;(2)不公平,理由见解析.
【解析】试题分析:(1)由把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲胜,乙胜的情况,即可求得求概率,比较大小,即可知这个游戏是否公平.
解:(1)由于三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,
故从袋中随机摸出一球,标号是1的概率为:;
(2)这个游戏不公平.
画树状图得:
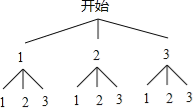
∵共有9种等可能的结果,两次摸出的球的标号之和为偶数的有5种情况,两次摸出的球的标号之和为奇数的有4种情况,
∴P(甲胜)=,P(乙胜)=.
∴P(甲胜)≠P(乙胜),
故这个游戏不公平.

练习册系列答案
相关题目




