题目内容
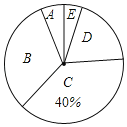
【题目】甘肃省注重建设“书香校园”.为了了解学生们的课外阅读情况,张老师调查了全班50名学生在一周内的课外阅读时间,并将统计的时间(单位:小时)分成5组:A.0.5≤x<1;B.1≤x<1.5;C.1.5≤x<2;D.2≤x<2.5;E.2.5≤x<3;并制成两幅不完整的统计图表如下:
组别 | 人数 | 占总数的百分比 |
A | 3 |
|
B |
|
|
C |
| 40% |
D | 9 |
|
E | 1 |
|
总计 | 50 | 100% |
请根据图表中提供的信息,解答下列问题:
(1)这次调查中学生课外阅读时间的中位数所在的组是 ;
(2)扇形统计图中,B组的圆心角为 ,并补全统计图表;
(3)请根据以上调查情况估计:全校1500名学生中有多少名学生每周阅读时间不低于2小时?
【答案】(1)C组;(2)122.4°,见解析;(3)300
【解析】
(1)先求出B、C组人数,再根据中位数的概念求解可得;
(2)根据以上所求B、C组数据,利用百分比的概念求解可补全图表;
(3)用总人数乘以样本中D、E组人数所占比例.
解:(1)C组的人数为:50×40%=20,
B组的人数为:50﹣3﹣20﹣9﹣1=17,
因为中位数是第25、26个数据的平均数,而这两个数据都在C组,
所以中位数在C组,
故答案为:C组.
(2)扇形统计图中,B组的圆心角为360°×![]() =122.4°,
=122.4°,
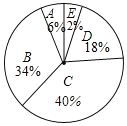
补全图表如下:
组别 | 人数 | 占总数的百分比 |
A | 3 | 6% |
B | 17 | 34% |
C | 20 | 40% |
D | 9 | 18% |
E | 1 | 2% |
总计 | 50 | 100% |
故答案为:122.4°;
(3)1500×![]() =300(名),
=300(名),
答:全校1500名学生中有300名学生每周阅读时间不低于2小时.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目