题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() .
.
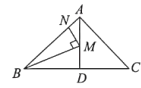
(1)如图所示,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上,且
上,且![]() ,当
,当![]() ,
,![]() 时,求线段
时,求线段![]() 的长;
的长;
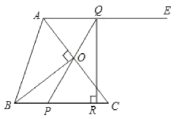
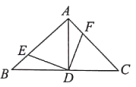
(2)如图所示,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,求证:
,求证:![]() ;
;
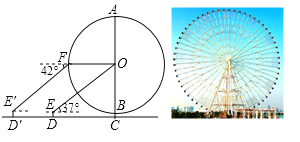
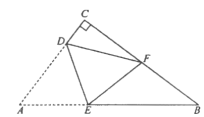
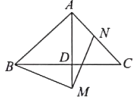
(3)如图所示,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且
上,且![]() ,请直接写出
,请直接写出![]() ,
,![]() ,
,![]() 三者的等量关系式.
三者的等量关系式.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)根据等腰三角形的性质、直角三角形的性质得到AD=BD=DC=![]() ,求出∠MBD=30°,根据勾股定理计算即可;
,求出∠MBD=30°,根据勾股定理计算即可;
(2)证明△BDE≌△ADF,根据全等三角形的性质证明;
(3)过点M作ME∥BC交AB的延长线于E,证明△BME≌△AMN,根据全等三角形的性质得到BE=AN,根据等腰直角三角形的性质、勾股定理证明结论.
(1)解:∵∠BAC=90°,AB=AC,AD⊥BC,
∴AD=BD=DC,∠ABC=∠ACB=45°,∠BAD=∠CAD=45°,
∵AB=2,
∴BC=![]()
∴AD=BD=DC=![]() BC=
BC=![]() ,
,
∵∠AMN=30°,
∴∠BMD=180°90°30°=60°,
∴∠MBD=30°,
∴BM=2DM,
由勾股定理得,BM2DM2=BD2,即(2DM)2DM2=(![]() )2,
)2,
解得,DM=![]() ,
,
∴AM=ADDM=![]()
![]() ;
;
(2)证明:∵AD⊥BC,∠EDF=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中,
 ,
,
∴△BDE≌△ADF(ASA)
∴BE=AF;
(3)![]() ,理由如下:
,理由如下:
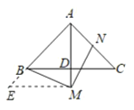
过点M作ME∥BC交AB的延长线于E,
∴∠AME=90°,∠E=90°-∠BAM=45°,
∴AM=EM,
则AE=![]() =
=![]() AM,
AM,
∵∠AME=90°,∠BMN=90°,
∴∠BME=∠AMN,
在△BME和△NMA中,
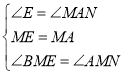 ,
,
∴△BME≌△NMA(ASA),
∴BE=AN,
∴AB+AN=AB+BE=AE=![]() AM.
AM.

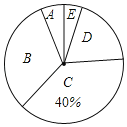
【题目】甘肃省注重建设“书香校园”.为了了解学生们的课外阅读情况,张老师调查了全班50名学生在一周内的课外阅读时间,并将统计的时间(单位:小时)分成5组:A.0.5≤x<1;B.1≤x<1.5;C.1.5≤x<2;D.2≤x<2.5;E.2.5≤x<3;并制成两幅不完整的统计图表如下:
组别 | 人数 | 占总数的百分比 |
A | 3 |
|
B |
|
|
C |
| 40% |
D | 9 |
|
E | 1 |
|
总计 | 50 | 100% |
请根据图表中提供的信息,解答下列问题:
(1)这次调查中学生课外阅读时间的中位数所在的组是 ;
(2)扇形统计图中,B组的圆心角为 ,并补全统计图表;
(3)请根据以上调查情况估计:全校1500名学生中有多少名学生每周阅读时间不低于2小时?