题目内容
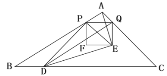
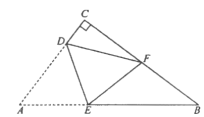
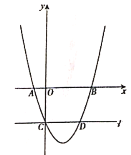
【题目】有一个著名的希波克拉蒂月牙问题:如图1,以直角三角形的各边为直径分别向上作半圆,则直角三角形的面积可表示成两个月牙形的面积之和,现将三个半圆纸片沿直角三角形的各边向下翻折得到图2,把较小的两张半圆纸片的重叠部分面积记为S1,大半圆纸片未被覆盖部分的面积记为S2,则直角三角形的面积可表示成( )
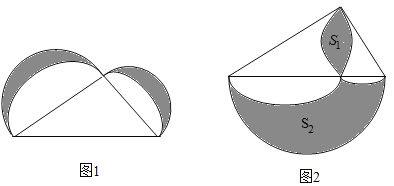
A.S1+S2B.S2﹣S1C.S2﹣2S1D.S1S2
【答案】B
【解析】
设以Rt△ABC的斜边为直径的半圆为大半圆,以AC为直径的半圆为中半圆,以BC为直径的半圆为小半圆,根据圆的面积公式和勾股定理进行解答即可.
解:设以Rt△ABC的斜边为直径的半圆为大半圆,以AC为直径的半圆为中半圆,以BC为直径的半圆为小半圆,
∵S小半圆=![]() π×
π×![]() =
=![]() BC2,S中半圆=
BC2,S中半圆=![]() AC2,S大半圆=
AC2,S大半圆=![]() AB2,
AB2,
∴S大半圆﹣S中半圆﹣S小半圆=![]() (AB2﹣BC2﹣AC2)=0,
(AB2﹣BC2﹣AC2)=0,
∵S△ABC+S大半圆﹣S中半圆﹣S小半圆+S1=S2,
∴S△ABC+S1=S2,
∴S△ABC=S2﹣S1,
∴直角三角形的面积可表示成S2﹣S1,
故选B.


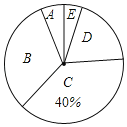
【题目】甘肃省注重建设“书香校园”.为了了解学生们的课外阅读情况,张老师调查了全班50名学生在一周内的课外阅读时间,并将统计的时间(单位:小时)分成5组:A.0.5≤x<1;B.1≤x<1.5;C.1.5≤x<2;D.2≤x<2.5;E.2.5≤x<3;并制成两幅不完整的统计图表如下:
组别 | 人数 | 占总数的百分比 |
A | 3 |
|
B |
|
|
C |
| 40% |
D | 9 |
|
E | 1 |
|
总计 | 50 | 100% |
请根据图表中提供的信息,解答下列问题:
(1)这次调查中学生课外阅读时间的中位数所在的组是 ;
(2)扇形统计图中,B组的圆心角为 ,并补全统计图表;
(3)请根据以上调查情况估计:全校1500名学生中有多少名学生每周阅读时间不低于2小时?
【题目】王妈妈在莲花商场里购买单价总和是90元的商品甲、乙、丙共两次,其中甲的单价是20元,乙的单价是40元,甲商品第一次购买的数量是第二次购买数量的两倍,乙商品第一次购买的数量与丙商品第二次购买的数量相等,两次购买商品甲、乙、丙的数量和总费用如下表:
购买商品甲的 数量(个) | 购买商品乙的 数量(个) | 购买商品丙的 数量(个) | 购买总费用(元) | |
第一次购物 | 4 | 440 | ||
第二次购物 | 7 | 490 |
(1)求两次购买甲、乙、丙三种商品的总数量分别是多少?
(2)由于莲花商场物美价廉,王妈妈打算第三次前往购买商品甲、乙、丙,设三种商品的数量总和为a个,其中购买乙商品数量是甲商品数量的3倍,购买总费用为1 280元,求a的最小值.