Question

【题目】如图，在矩形中，分别是边上的点，，将沿所在直线折叠，点的对应点正好落在线段上，若，则折痕的长为__________．

Answer 1

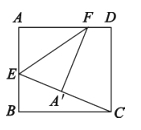
【答案】

【解析】

连接FC，利用折叠的性质可得A'E=AE=6，在Rt△BEC中求得BC=12，然后设AF=x，利用CF2=CD2+DF2=A'F2+A'C2列出方程求得AF的长，最后在Rt△ＡＥＦ中，利用勾股定理求得ＥＦ的长即可．

解：如图，连接FC，

在矩形ABCD中，∠A=∠B=∠D=90°，AB=CD，AD=BC，

∵

∴CD=AB=AE+BE=11，

∵折叠，

∴∠A'=∠A=90°，A'E=AE=6，A'F=AF，

∵A'C=7，

∴EC= A'C+ A'E=13，

又∵BE=5，

∴在Rt△BEC中，BC=，

∴AD=BC=12，

设AF= A'F=x，则DF=12-x，

∵CF2=CD2+DF2=A'F2+A'C2，

∴112+（12-x）2=x2+72，

解得x=9，

∴在Rt△AEF中，EF=，

故答案为：．