题目内容
【题目】如图,AB是半圆O的直径,AD为弦,∠DBC=∠A.

(1)求证:BC是半圆O的切线;
(2)若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
【答案】(1)见解析;(2)AD=4.5.
【解析】
(1)若证明BC是半圆O的切线,利用切线的判定定理:即证明AB⊥BC即可;
(2)因为OC∥AD,可得∠BEC=∠D=90°,再有其他条件可判定△BCE∽△BAD,利用相似三角形的性质:对应边的比值相等即可求出AD的长.
(1)证明:∵AB是半圆O的直径,
∴BD⊥AD,
∴∠DBA+∠A=90°,
∵∠DBC=∠A,
∴∠DBA+∠DBC=90°即AB⊥BC,
∴BC是半圆O的切线;
(2)解:∵OC∥AD,
∴∠BEC=∠D=90°,
∵BD⊥AD,BD=6,
∴BE=DE=3,
∵∠DBC=∠A,
∴△BCE∽△BAD,
![]() ,即
,即![]() ;
;
∴AD=4.5

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
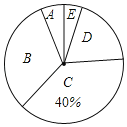
【题目】甘肃省注重建设“书香校园”.为了了解学生们的课外阅读情况,张老师调查了全班50名学生在一周内的课外阅读时间,并将统计的时间(单位:小时)分成5组:A.0.5≤x<1;B.1≤x<1.5;C.1.5≤x<2;D.2≤x<2.5;E.2.5≤x<3;并制成两幅不完整的统计图表如下:
组别 | 人数 | 占总数的百分比 |
A | 3 |
|
B |
|
|
C |
| 40% |
D | 9 |
|
E | 1 |
|
总计 | 50 | 100% |
请根据图表中提供的信息,解答下列问题:
(1)这次调查中学生课外阅读时间的中位数所在的组是 ;
(2)扇形统计图中,B组的圆心角为 ,并补全统计图表;
(3)请根据以上调查情况估计:全校1500名学生中有多少名学生每周阅读时间不低于2小时?