Question

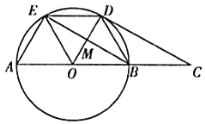
【题目】随着天气的逐渐炎热（如图1），遮阳伞在我们的日常生活中随处可见如图2所示，遮阳伞立柱OA垂直于地面，当将遮阳伞撑开至OD位置时，测得∠ODB＝45°，当将遮阳伞撑开至OE位置时，测得∠OEC＝30°，且此时遮阳伞边沿上升的竖直高度BC为20cm，求若当遮阳伞撑开至OE位置时伞下阴凉面积最大，求此时伞下半径EC的长．（结果保留根号）

Answer 1

【答案】20（）cm

【解析】

根据题意可得OE＝OD，由三角函数得出OC＝OE，OB＝，再利用BC＝OB﹣OC解答即可．

解：由题意可得：OE＝OD，

在Rt△OEC中，∠BOE＝60°，∠OCE＝90°，

∴OC＝OE，

在Rt△OBD中，∠DOB＝45°，∠OBD＝90°，

∴OB＝OD＝OE，

∵BC＝OB﹣OC，

即，OE﹣OE＝20

解得：OE＝40（+1）cm，

∴EC＝×20（+1）＝20（）cm．