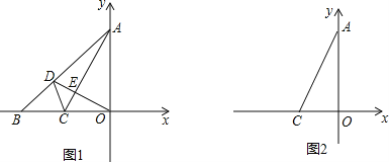题目内容
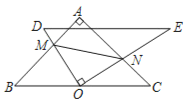
【题目】笑笑将一副三角板按如图所示的位置放置,△DOE的直角顶点O在边BC的中点处,其中∠A=∠DOE=90°.∠B=45°,∠D=60°,△DOE绕点O自由旋转,且OD,OE分别交AB,AC于点M,N当AN=4,NC=2时,MN的长为_____.
【答案】2![]()
【解析】
如图,连接AO,作OH⊥AC于H.首先证明△OMN是等腰直角三角形,求出ON即可解决问题.
解:如图,连接AO,作OH⊥AC于H.
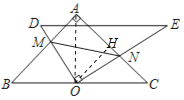
∵AB=AC,∠BAC=90°,O为BC的中点,
∴AO⊥BC,∠BAO=∠C=45°,OA=OB=OC,
∵∠DOE=∠AOC=90°,
∴∠AOM=∠CON,
∴△AOM≌△CON(SAS),
∴OM=ON,
∵AN=4,NC=2,
∴AC=6,
∵∠AOC=90°,OA=OC,OH⊥AC,
∴AH=HC=3,OH=AH=CH=3,
∴HN=AN﹣AH=4﹣3=1,
∴![]()
∴![]()
故答案为2![]() .
.

练习册系列答案
相关题目
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?