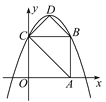题目内容
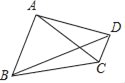
【题目】如图,在四边形ABCD中,AC、BD是对角线,AC=AD,BC>AB,AB∥CD,AB=4,BD=2![]() ,tan∠BAC=3
,tan∠BAC=3![]() ,则线段BC的长是_____.
,则线段BC的长是_____.
【答案】6
【解析】
作DE⊥AB,交BA的延长线于E,作CF⊥AB,可得DE=CF,且AC=AD,可证Rt△ADE≌Rt△AFC,可得AE=AF,∠DAE=∠BAC,根据tan∠BAC=∠DAE=![]() ,可设DE=3
,可设DE=3![]() a,AE=a,根据勾股定理可求a的值,由此可得BF,CF的值.再根据勾股定理求BC的长.
a,AE=a,根据勾股定理可求a的值,由此可得BF,CF的值.再根据勾股定理求BC的长.
如图:
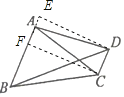
作DE⊥AB,交BA的延长线于E,作CF⊥AB,
∵AB∥CD,DE⊥AB⊥,CF⊥AB
∴CF=DE,且AC=AD
∴Rt△ADE≌Rt△AFC
∴AE=AF,∠DAE=∠BAC
∵tan∠BAC=3![]()
∴tan∠DAE=3![]()
∴设AE=a,DE=3![]() a
a
在Rt△BDE中,BD2=DE2+BE2
∴52=(4+a)2+27a2
解得a1=1,a2=-![]() (不合题意舍去)
(不合题意舍去)
∴AE=1=AF,DE=3![]() =CF
=CF
∴BF=AB-AF=3
在Rt△BFC中,BC=![]() =6
=6

练习册系列答案
相关题目
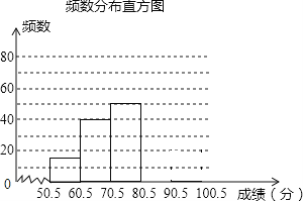
【题目】 某校为加强学生安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)进行统计,请根据尚为完成的频率和频数分布直方图,解答下列问题:
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.35 |
90.5~100.5 | 24 | n |
(1)这次抽取了______名学生的竞赛成绩进行统计,其中m=______,n=______;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?