题目内容
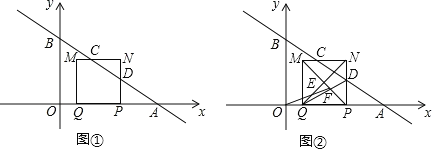
【题目】如图，在平面直角坐标系中，OA=OB，△OAB的面积是2．
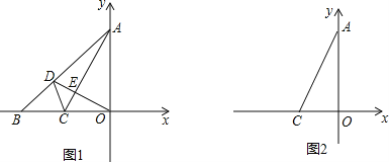
（1）求线段OB的中点C的坐标．
（2）连结AC，过点O作OE⊥AC于E，交AB于点D．
①直接写出点E的坐标．
②连结CD，求证：∠ECO=∠DCB；
（3）点P为x轴上一动点，点Q为平面内一点，以点A.C.P.Q为顶点作菱形，直接写出点Q的坐标．
【答案】（1）线段OB的中点C的坐标为：（-1，0）；（2）①点E坐标为：（-
，
）；②详见解析；（3）点Q的坐标为：（0，-2）.（-
，2）.（，2），（-
，2）
【解析】
（1）由OA=OB，△OAB的面积是2，可求得OB的长度，由C为OB中点，即可得C点坐标；
（2）①过点E作EF⊥OB，由
，设EF=x，借助勾股定理即可求解；②过点B作OB的垂线，交OE的延长线于点G，先证△AOC≌△OBG，再证△BGD≌△BCD，再根据等量代换可证；
（3）以点C和点A 为圆心，以
为半径作圆和作AC的垂直平分线分情况讨论求解即可．
解：（1）∵OA=OB，△OAB的面积是2．
∴
OAOB=2，
∴OA=OB=2，
∴线段OB的中点C的坐标为：（-1，0），
（2）①过点E作EF⊥OB，
∵∠AOC=90°，OA=2，OC=1，
∴AC=，
∵OE⊥AC，由面积法得：OE=
=
=
，
∵∠EOF+∠AOE=∠EAO+∠AOE=90°，
∴∠EOF=∠EAO，
∴tan∠EOF=tan∠EAO=，设EF=x，则OF=2x，
∴由勾股定理得：
，
解得：x=
，2x=
，
∴点E坐标为：（-，）．
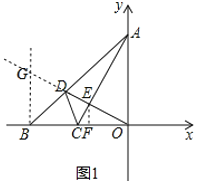
②证明：过点B作OB的垂线，交OE的延长线于点G，由（2）①可知，∠EOF=∠EAO，
∴在△AOC和△OBG中，
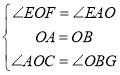
∴△AOC≌△OBG（ASA），
∴∠ECO=∠BGD，BG=OC，
∵C为线段OB的中点，
∴BG=BC，
∵OA=OB，∠AOC=∠OBG=90°，
∴∠GBD=∠CBD=45°，
∴在△BGD和△BCD中，
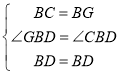
∴△BGD≌△BCD（SAS）
∴∠DCB=∠BGD，
又∠ECO=∠BGD，
∴∠ECO=∠DCB．
（3）∵AC=，
∴以点A为圆心，以为半径作圆，与x轴可得一个交点P1（1，0），从而得Q1（0，-2）；
∴以点C为圆心，以为半径作圆，与x轴可得两个交点P2（-
，0），P3（，0），从而得Q2（-，2），Q3（，2），
由tan∠ACO=2，可知，
当以AC为菱形的对角线时，AC被另一条对角线垂直平分，
，从而另一条对角线P4Q4的一半为，从而P4C=
，
∴P4（
，0），Q4（-，2）
综上，点Q的坐标为：（0，-2）．（-，2）．（，2），（-，2）．
