题目内容
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
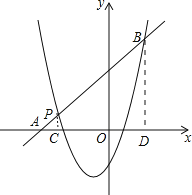
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
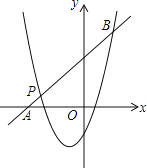
【答案】(1)m=2,n=2,(2)y=x+4;(3)x<-3或x>2
【解析】(1)∵对称轴是经过(1,0)且平行于y轴的直线,
∴![]() ,
,
∴m=2,
∵二次函数y=x2+mx+n的图象经过点P(3,1),
∴93m+n=1,得出n=3m8.
∴n=3m8=2;
(2)∵m=2,n=2,
∴二次函数关系式为y=x2+2x2,
过P作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,
∴![]() ,
,
∵P (3,1),
∴PC=1,
∵PA:PB=1:5,
∴![]() ,
,
∴BD=6,
∴B的纵坐标为6,
代入二次函数为y=x2+2x2得,6=x2+2x2,
解得![]() =2,
=2,![]() =4(舍去),
=4(舍去),
∴B(2,6),
一次函数y2=kx+b经过了点B(2,6)、P(-3,1)则
![]()
解得![]()
∴一次函数的表达式为y=x+4
(3)x<-3或x>2

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目