题目内容
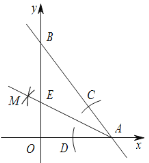
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
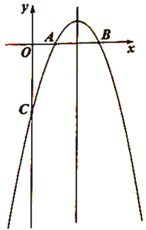
(1)求该抛物线的解析式;
(2)绕点![]() 旋转的直线
旋转的直线![]() :
:![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,且满足
,且满足![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)点![]() 为抛物线上的一点,点
为抛物线上的一点,点![]() 为抛物线对称轴上的一点,是否存在以点
为抛物线对称轴上的一点,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的平行四边形,若存在,请直接写出点
为顶点的平行四边形,若存在,请直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)抛物线的解析式为:![]() ;(2)直线
;(2)直线![]() 的解析式为
的解析式为![]() 或
或![]() ;(3)存在,符合题意的点
;(3)存在,符合题意的点![]() 有3个:
有3个:![]() ,
,![]() ,
,![]()
【解析】
(1把![]() 和
和![]() 代入
代入![]() 中得到一个关于a,b的二元一次方程组,把这个方程组解出来即可;
中得到一个关于a,b的二元一次方程组,把这个方程组解出来即可;
(2)分两种情况讨论进行计算即可;
(3)分三种情况讨论,利用平行四边形的性质列方程求解即可.
解:(1)∵抛物线经过点![]() ,点
,点![]() ,
,
∴![]() 解得:
解得:![]()
∴抛物线的解析式为:![]()
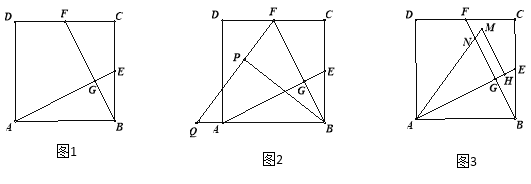
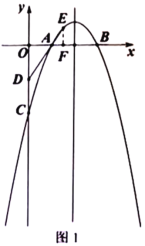
(2)①如图1,当点![]() 、
、![]() 在点
在点![]() 的异侧时,过点
的异侧时,过点![]() 作
作![]() 轴于点
轴于点![]()
∴![]()
∵![]()
∴![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴点![]() 与点
与点![]() 的横坐标为
的横坐标为![]()
∴点![]() 的纵坐标为
的纵坐标为![]()
![]() ∴点
∴点![]() 的坐标为
的坐标为![]()
∵直线![]() :
:![]() 过点
过点![]() 和点
和点![]()
∴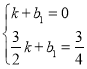 解得:
解得: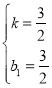
∴直线![]() 的解析式为
的解析式为![]()
②如图2,当点![]() 、
、![]() 在点
在点![]() 的同侧时,过点
的同侧时,过点![]() 作
作![]() 轴于点
轴于点![]()
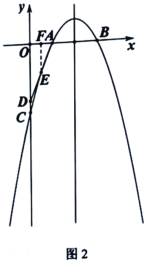
∴![]()
∵![]()
∴![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴点![]() 与点
与点![]() 的横坐标为
的横坐标为![]()
∴点![]() 的纵坐标为
的纵坐标为![]()
∴点![]() 的坐标为
的坐标为![]()
∵直线![]() :
:![]() 过点
过点![]() 和点
和点![]()
∴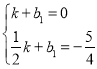 解得:
解得: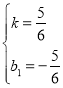
∴直线![]() 的解析式为
的解析式为![]()
综上所述:直线![]() 的解析式为
的解析式为![]() 或
或![]() .
.
(3)存在,符合题意的点![]() 有3个它们分别是:
有3个它们分别是:![]() ,
,![]() ,
,![]() .
.
设P的坐标为P(x, ![]() ),点Q的坐标为(2,y)
),点Q的坐标为(2,y)
当BP∥CQ时,则![]() ,解得x=1,
,解得x=1,
∴![]() =
=![]()
∴![]() .
.
当BP∥QC时,则![]() ,解得x=5,
,解得x=5,
∴![]() =
=![]()
∴![]() ,
,
③当BC∥PQ时,则![]() ,解得x=-1,
,解得x=-1,
∴![]() =
=![]()
∴![]() .
.
综上所述,点![]() 有3个它们分别是:
有3个它们分别是:![]() ,
,![]() ,
,![]() .
.
【点晴】
本题考查了二次函数的综合应用,合理利用数形结合和分类讨论是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目