题目内容
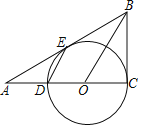
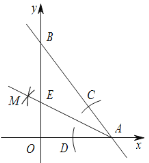
【题目】如图，在四边形
中，
，以BC为直径的⊙O交AD于点E，且
，则图中阴影部分的面积是___________
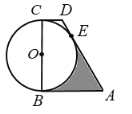
【答案】9
－3π
【解析】
过点D作DF⊥AB，由勾股定理可求得FA的长，进而求出∠DAF=60°，连接OA，OE，可证得△OBA≌△OEA，所以∠OAB=30°，则AB，CD的长都可以求得，再由
即可求出阴影部分面积．
连接OA，OE，过点D作DF⊥AB，交AB于F，如图，
∵
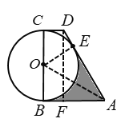
，DF⊥AB，
∴四边形BCDF是矩形，
∴DF=BC=6，
在Rt△DFA中，由勾股定理得，
,
∴
，
∴∠DAF=60°，
∵在△OBA与△OEA中，
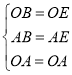
∴△OBA≌△OEA，
∴∠OAE=∠OAB=30°，∠OBA=∠OEA=90°，
∴∠BOE=120°，
∴
,
∵CD=DE，
∴
,
,
故答案为：
．
练习册系列答案
相关题目
