Question

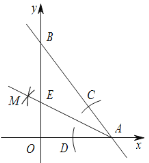
【题目】已知抛物线y＝x2﹣bx+c（b，c为常数，b＞0）经过点A（﹣1，0），点M（m，0）是x轴正半轴上的动点．

（1）当b＝2时，求抛物线的顶点坐标；

（2）点D（b，yD）在抛物线上，当AM＝AD，m＝3时，求b的值；

（3）点Q（b+，yQ）在抛物线上，当AM+2QM的最小值为时，求b的值．（说明：yD表示D点的纵坐标，yQ表示Q点的纵坐标）

Answer 1

【答案】（1）；（2）；（3）6．

【解析】

（1）将点A坐标及b的值代入可得抛物线解析式，化为顶点式可得顶点坐标.

（2）将点D横坐标代入可得其纵坐标yD＝﹣b﹣1，由b＞0可判断其所在象限，过点D作DE⊥x轴，垂足为E，则点E（b，0），表示出AE、DE长，可知AE＝DE，在Rt△ADE中，得AD＝AE，由AM＝AD求出b值即可；

（3）求出yQ，可知点Q（b+，﹣﹣）在第四象限，且在直线x＝b的右侧，可取点N（0，1），过点Q作直线AN的垂线，垂足为G，QG与x轴相交于点M，过点Q作QH⊥x轴于点H，则点H（b+，0），在Rt△MQH中，可知∠QMH＝∠MQH＝45°，设点M（m，0），可用含b的代数式表示m，由AM+2QM＝列出方程求解即可.

解：（1）∵抛物线y＝x2﹣bx+c经过点A（﹣1，0），

∴1+b+c＝0，

即c＝﹣b﹣1，

当b＝2时，

y＝x2﹣2x﹣3＝（x﹣1）2﹣4，

∴抛物线的顶点坐标为（1，﹣4）；

（2）由（1）知，抛物线的解析式为y＝x2﹣bx﹣b﹣1，

∵点D（b，yD）在抛物线y＝x2﹣bx﹣b﹣1上，

∴yD＝b2﹣bb﹣b﹣1＝﹣b﹣1，

由b＞0，得b＞＞0，﹣b﹣1＜0，

∴点D（b，﹣b﹣1）在第四象限，且在抛物线对称轴x＝的右侧，

如图1，过点D作DE⊥x轴，垂足为E，则点E（b，0），

∴AE＝/span>b+1，DE＝b+1，得AE＝DE，

∴在Rt△ADE中，∠ADE＝∠DAE＝45°，

∴AD＝AE，

由已知AM＝AD，m＝3，

∴3﹣（﹣1）＝（b+1），

∴b＝2﹣1；

（3）∵点Q（b+，yQ）在抛物线y＝x2﹣bx﹣b﹣1上，

∴yQ＝（b+）2﹣b（b+）﹣b﹣1＝﹣﹣，

可知点Q（b+，﹣﹣）在第四象限，且在直线x＝b的右侧，

∵AM+2QM＝2（AM+QM），

∴可取点N（0，1），

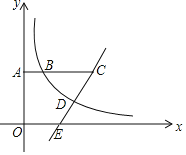
如图2，过点Q作直线AN的垂线，垂足为G，QG与x轴相交于点M，

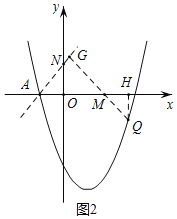
由∠GAM＝45°，得AM＝GM，

则此时点M满足题意，

过点Q作QH⊥x轴于点H，则点H（b+，0），

在Rt△MQH中，可知∠QMH＝∠MQH＝45°，

∴QH＝MH，QM＝MH，

∵点M（m，0），

∴0﹣（﹣﹣）＝（b+）﹣m，

解得m＝﹣，

∵AM+2QM＝，

∴[（﹣）﹣（﹣1）]+2[（b+）﹣（﹣）]＝，

∴b＝6．