题目内容
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() .
.
(1)求![]() 的值;
的值;
(2)若点![]() 是直线
是直线![]() 上方抛物线的一部分上的动点,过点P作
上方抛物线的一部分上的动点,过点P作![]() 轴于点F,交直线AB于点D,求线段
轴于点F,交直线AB于点D,求线段![]() 的最大值
的最大值
(3)在(2)的条件下,连接![]() ,点
,点![]() 是抛物线对称轴上的一动点,在抛物线上是否存在点
是抛物线对称轴上的一动点,在抛物线上是否存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

【答案】(1)b=-![]() ,c=3;(2)
,c=3;(2)![]() ;(3)存在,G(1,
;(3)存在,G(1,![]() )或(-5,-
)或(-5,-![]() )或(3,-
)或(3,-![]() )
)
【解析】
(1)先根据直线![]() 求得点A,B的坐标,代入到二次函数
求得点A,B的坐标,代入到二次函数![]() 中,建立关于b,c的二元一次方程求解即可;
中,建立关于b,c的二元一次方程求解即可;
(2)设点P(m,-![]() m-
m-![]() m+3),则D(m,
m+3),则D(m,![]() m+3),用含m的代数式表示线段PD的长,转化为二次函数的问题求其最大值;
m+3),用含m的代数式表示线段PD的长,转化为二次函数的问题求其最大值;
(3)分CD为平行四边形的对角线和边两种情况,分类讨论,并结合中点坐标公式及平行四边形及平移的性质,计算求解即可.
解:(1)由![]() 得, 当
得, 当![]() 时,y=3;当
时,y=3;当![]() 时,
时,![]() ,
,
即![]() 与坐标轴的交点坐标为
与坐标轴的交点坐标为![]()
分别将![]() 代入
代入![]() ,
,
得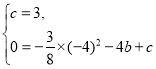
解得,b=-![]() ,c=3.
,c=3.
(2)由(1)得y=-![]() x-
x-![]() x+3,
x+3,
设点P(m,-![]() m-
m-![]() m+3),
m+3),
则D(m,![]() m+3)
m+3)
∴PD=-![]() m-
m-![]() m+3-(
m+3-(![]() m+3)=-
m+3)=-![]() m-
m-![]() m=-
m=-![]() (m+2)+
(m+2)+![]()
所以当m=-2时,PD最大,最大值是![]() .
.
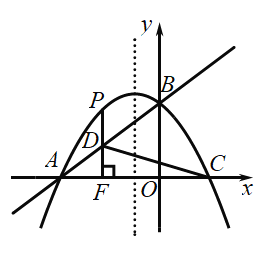
(3)存在点G ,使得以C、D、G、Q为顶点的四边形是平行四边形.他们分别是:G(1,![]() )或G(3,-
)或G(3,-![]() )或G(-5,-
)或G(-5,-![]() ).理由如下:
).理由如下:
由(2)得 m=-2时,点D(-2,![]() ),由二次函数
),由二次函数![]() 可求得点C(2,0),对称轴为x=-1
可求得点C(2,0),对称轴为x=-1
设G(n,-![]() n-
n-![]() n+3),Q(-1,p),CD与y轴交于点E,显然E为CD中点.
n+3),Q(-1,p),CD与y轴交于点E,显然E为CD中点.
①当CD为对角线时,对角线QE的中点即为点E,由中点坐标公式可得:
n+(-1)=0,所以n=1,此时点G(1,![]() )
)
②当CD为边时,
i)若G在Q上边,由平行四边形及平移的性质可知,点D向右平移4个单位,向下平移![]() 个单位到点C,故点G也同样的平移到点Q, 则n+4=-1,则n=-5,此时点G(-5,-
个单位到点C,故点G也同样的平移到点Q, 则n+4=-1,则n=-5,此时点G(-5,-![]() ).
).
ii)若G在Q下边,由平行四边形及平移的性质可知,点D向右平移4个单位,向下平移![]() 个单位到点C,故点Q也同样的平移到点G,则-1+4=n,则n=3,此时点G(3,-
个单位到点C,故点Q也同样的平移到点G,则-1+4=n,则n=3,此时点G(3,-![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】某校举行汉字听写大赛,学习对参赛者获奖情况进行统计,根据比赛成绩列出统计表,并绘制了扇形统计图
(1)参加此次比赛的学生共______________人.
(2)![]()
(3)若从一等奖中随机抽取两名学生,参加市级汉字听写大赛,请用树状图或列表的方法,求出所选的两名学生正好为一男一女的概率.
等次 | 男生 | 女生 |
一等奖 | 3 | m |
二等奖 | 6 | 12 |
三等奖 | 8 | 9 |
鼓励奖 | 6 | n |

【题目】某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合计 | a |
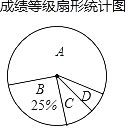
(1)表中a= ,b= ;
(2)扇形图中C的圆心角度数是 ;
(3)若该校共有九年级男生600人,请估计没有获得A等级的学生人数.