题目内容
【题目】刘徽计算圆周率是从正六边形开始的，易知圆的内接正六边形可分为六个全等的正三角形，每个三角形的边长均为圆的半径
．此时圆内接正六边形的周长为
，如果将圆内接正六边形的周长等同于圆的周长，可得圆周率为3．当正十二边形内接于圆时，如果按照上述方法计算，可得圆周率为______．（参考数据：
）
【答案】3.12
【解析】
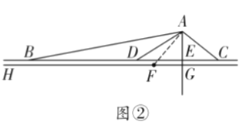
连接OA1、OA2，根据正十二边形的性质得到∠A1OA2=30°，△A1OA2是等腰三角形，作OM⊥A1A2于M，根据等腰三角形三线合一的性质得出∠A1OM=15°，A1A2=2A1M．设圆的半径R，解直角△A1OM，求出A1M，进而得到正十二边形的周长L，那么圆周率
．
如图，设半径为R的圆内接正十二边形的周长为L．
连接OA1、OA2，
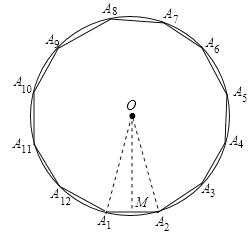
∵十二边形A1A2…A12是正十二边形，
∴∠A1OA2=30°．
作OM⊥A1A2于M，又OA1=OA2，
∴∠A1OM=15°，A1A2=2A1M．
在直角△A1OM中，A1M=OA1sin∠A1OM=0.26R，
∴A1A2=2A1M=0.52R，
∴L=12A1A2=6.24R，
∴圆周率
．
故答案为3.12．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
