题目内容
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点G,如图,当点G运动到某位置时,以AG,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点G的坐标;
(3)若抛物线上存在点P,使得△ACP是以AC为直角边的直角三角形,直接写出所有符合条件的点P的坐标.

【答案】(1)抛物线的解析式为y=﹣x2+3x+4;(2)点G的坐标为(![]() ,
,![]() );(3)点P(2,6)或(﹣2,﹣6).
);(3)点P(2,6)或(﹣2,﹣6).
【解析】
(1)由点A的坐标及OA=OC=4OB,可得出点B,C的坐标, 根据点A,B,C的坐标,利用待定系数法即可求出抛物线的解析式;
(2)由二次函数的解析式利用二次函数的性质可得出抛物线的对称轴, 由AO的长度结合平行四边形的性质可得出点G的横坐标, 再利用二次函数图象上点的坐标特征,即可求出点G的坐标;
(3)设点P的坐标为(m,-m2+3m+4),结合点A,C的坐标可得出AP2,CP2,AC2的值, 分∠ACP=90°及∠PAC=90°两种情况, 利用勾股定理即可得出关于m的一元二次方程,解之即可得出结论.
解:(1)∵点A的坐标是(4,0),
∴OA=4,
又∵OA=OC=4OB,
∴OA=OC=4,OB=1,
∴点C的坐标为(0,4),点B的坐标为(﹣1,0).
设抛物线的解析式为y=ax2+bx+c(a≠0),
将A(4,0),B(﹣1,0),C(0,4)代入y=ax2+bx+c,
得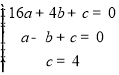 ,解得:
,解得: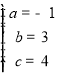 ,
,
∴抛物线的解析式为y=﹣x2+3x+4,
(2)∵抛物线的解析式为y=﹣x2+3x+4,
∴抛物线的对称轴为直线x=![]() ,
,
∵如图1,动点G在AC上方的抛物线上,且以AG,AO为邻边的平行四边形的第四个顶点H也在抛物线上,

∴GH∥AO,GH=AO=4,
∵点G,H都在抛物线上,
∴G,H关于直线x=![]() 对称,
对称,
∴点G的横坐标为![]() ,
,
∵当x=![]() 时,y=﹣x2+3x+4=
时,y=﹣x2+3x+4=![]() ,
,
∴点G的坐标为(![]() ,
,![]() ).
).
(3)假设存在,设点P的坐标为(m,-m2+3m+4),
∴AP2=(m-4)2+(-m2+3m+4-0)2=m4-6m3+2m2+16m+32,
CP2=(m-0)2+(-m2+3m+4-4)2=m4-6m3+10m2,AC2=(0-4)2+(4-0)2=32,
分两种情况考虑,如图2所示,
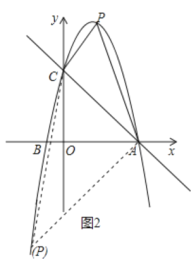
①当∠ACP=90°时,AP2=CP2+AC2,
即m4-6m3+2m2+16m+32=m4-6m3+10m2+32, 整理得:m2-2m=0,
解得:m1=0(舍去),m2=2,
∴点P的坐标为(2,6);
整理得:m2-2m-8=0,解得:m3=-2,m4=4(舍去),
∴点P的坐标为(-2,-6).
综上所述,假设成立,抛物线上存在点P(2,6)或(﹣2,﹣6),使得△ACP是以为直角边的直角三角形.

 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案