题目内容
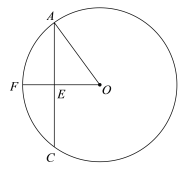
【题目】已知:如图,AO是![]() 的半径,AC为
的半径,AC为![]() 的弦,点F为
的弦,点F为![]() 的中点,OF交AC于点E,AC=8,EF=2.
的中点,OF交AC于点E,AC=8,EF=2.
(1)求AO的长;
(2)过点C作CD⊥AO,交AO延长线于点D,求sin∠ACD的值.
【答案】(1)5;(2)![]()
【解析】
(1)由垂径定理得出AE=4,设圆的半径为r,知OE=OF-EF=r-2,根据OA2=AE2+OE2求解可得;
(2)由∠OAE=∠CAD,∠AEO=∠ADC=90°知∠AOE=∠ACD,从而根据sin∠ACD=sin∠AOE=![]() 可得答案.
可得答案.
(1)∵O是圆心,且点F为![]() 的中点,
的中点,
∴OF⊥AC,
∵AC=8,
∴AE=4,
设圆的半径为r,即OA=OF=r,
则OE=OF-EF=r-2,
由OA2=AE2+OE2得r2=42+(r-2)2,
解得:r=5,即AO=5;
(2)如图:
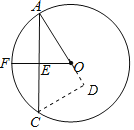
∵∠OAE=∠CAD,∠AEO=∠ADC=90°,
∴∠AOE=∠ACD,
则sin∠ACD=sin∠AOE=![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目