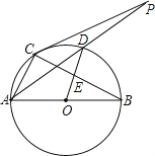
��Ŀ����
����Ŀ����ͼ����ACL��90����AC��4������B������CL��CH��AB�ڵ�H����HΪԲ�ģ�HBΪ�뾶��Բ������BA�ڵ�D����ֱ��CD�ڵ�F����ֱ��BC�ڵ�E����BC��m��

��1������A��30��ʱ�����CDB�Ķ�����
��2����m��2ʱ����BE�ij��ȣ�
��3���ڵ�B�������˶������У�
�ٵ�BC��3CEʱ��������з���������m��ֵ��
������EH��FH����tan��FHE��![]() ʱ��ֱ��д����FHD���EFH����ȣ�
ʱ��ֱ��д����FHD���EFH����ȣ�
���𰸡���1��60������2��![]() ����3����m��2
����3����m��2![]() ��4
��4![]() ����
����![]()
��������
��1������������HB��HD��CH��BD��֪��CH��BD���д��ߣ�������A��30���ã���CDB����ABC��60����
��2���������֪��m��2ʱ���ɹ��ɶ����ɵã�AB��2![]() ��cos��ABC��
��cos��ABC��![]() ������H��HK��BC�ڵ�K�����ô��������ɵý��ۣ�
������H��HK��BC�ڵ�K�����ô��������ɵý��ۣ�
��3������Ҫ�����������I������E��C�Ҳ�ʱ��II������E��C���ʱ�������������������ʺ��ɶ���������ý��ۣ�
������������֤��EF��BD������ƽ���������ȿɵã���FHD����EFH����ȣ�����ȵ��ڵ�֮�ȣ�����tan��FHE��![]() �����
�����![]() ��ֵ���ɣ�
��ֵ���ɣ�
�⣺��1���ߡ�A��30������ACB��90����
���ABC��60����
��HB��HD��CH��BD��
��CH��BD���д��ߣ�
��CB��CD��
���CDB����ABC��60����
��2����ͼ1������H��HK��BC�ڵ�K��

��m��2ʱ��BC��2��
��AB��![]() ��2
��2![]() ��
��
��cos��ABC��![]() ��
��![]() ��
��
��BH��BCcos��ABC��![]() ��
��
��BK��BHcos��ABC��![]() ��
��
��BE��2BK��![]() ��
��
��3���������������
I������E��C�Ҳ�ʱ����ͼ2������DE����BD��ֱ������DE��BC��

��BC��3CE��m��
��CE��![]() m��BE��
m��BE��![]() m��
m��
��DE��AC��
���DEB����ACB��
��![]() ��
��![]() ��
��![]() ��
��
��DE��![]() AC��
AC��![]() ��
��
��CD��CB��m��
��Rt��CDE�У��ɹ��ɶ����ã� ��m2��
��m2��
��m��0��
��m��2![]() ��
��
II������E��C���ʱ����ͼ3������DE����BD��ֱ������DE��BC��

��BC��3CE��
��CE��![]() m��BE��
m��BE��![]() m��
m��
��DE��AC��
���DEB����ACB��
��![]() ��
��![]() ��
��![]() ��
��
��DE��![]() AC��6��
AC��6��
��CD��CB��m��
��Rt��CDE�У��ɹ��ɶ����ã�62+ ��m2��
��m2��
��m��0��
��m��4![]() ��
��
��������������BC��3CEʱ��m��2![]() ��4
��4![]() ��
��
����ͼ4����F��FG��HE�ڵ�G��

��CH��AB��HB��HD��
��CB��CD��
���CBD����CDB��
��![]() ����
����![]() ��
��
��![]() ��
��
��EF��BD��
��![]() ��
��![]() ��
��
����Rt��FHG��![]() ��tan��FHE��
��tan��FHE��![]() ��
��
��FG��5k��HG��12k����FH��![]() ��
��![]() ��13k��
��13k��
��DH��HE��FH��13k��EG��HE��HG��13k��12k��k��
��EF��![]() ��
��![]() ��
��![]() k��
k��
��![]() ��
��![]() ��
��![]() ��
��

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
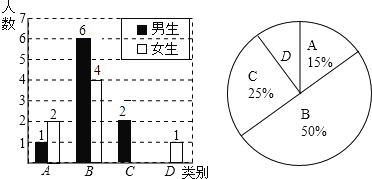
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�����Ŀ��ij��˾����![]() �������ţ�����ÿ�����ŵ�Ա����������Ӧÿ����������������Ƴ����µ�ͳ�Ʊ�������ͼ��
�������ţ�����ÿ�����ŵ�Ա����������Ӧÿ����������������Ƴ����µ�ͳ�Ʊ�������ͼ��

������������ÿ������������ͳ�Ʊ�
���� | Ա������ | ÿ��������������/��Ԫ |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
��1����������ͼ�У�C��������Ӧ��Բ�ĽǵĶ���Ϊ___________��
����ͳ�Ʊ��У�![]() ___________��
___________��![]() ___________��
___________��
��2���������˾ƽ��ÿ������������