Question

【题目】如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2，Q为AC上的动点，P为Rt△ABC内一动点，且满足∠APB=120°，若D为BC的中点，则PQ+DQ的最小值是（　　）

A. B. C. 4D.

Answer 1

【答案】A

【解析】

根据题意作以AB为边，向左边作等边△ABE，作△ABE的外接圆⊙O，连接OB，则点P在⊙O上．得到OB=4，OB⊥BC，再作点D关于AC的对称点D′，连接OD′，OP，PD′，PD′交AC于Q，得到PQ+QD=PQ+QD′=PD′，根据勾股定理进行解答即可

解：如图以AB为边，向左边作等边△ABE，作△ABE的外接圆⊙O，连接OB，则点P在⊙O上．

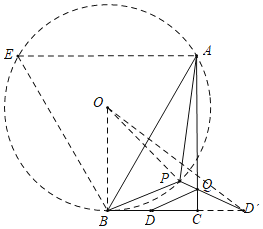
在Rt△ABC中，∵∠ACB=90°，∠ABC=60°，BC=2，

∴AB=4 ，

则易知OB=4，OB⊥BC，

作点D关于AC的对称点D′，连接OD′，OP，PD′，PD′交AC于Q，则PQ+QD=PQ+QD′=PD′，

∵PD′≥OD′-OP，OP=OB=4，OD′= = ，

∴PD′≥-4，

∴PQ+DQ的最小值为-4，

故选：A．