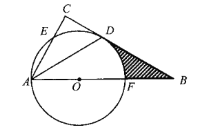
题目内容
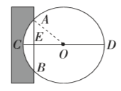
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径的圆恰好经过点
为半径的圆恰好经过点![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]()
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)若![]() ,
,![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() )
)
【答案】(1)![]() 与
与![]() 相切,见解析;(2)
相切,见解析;(2)![]()
【解析】
(1)连接OD,证明OD∥AC,即可证得∠ODB=90°,从而证得BC是圆的切线;
(2)在直角三角形OBD中,设![]() ,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,进而求出圆心角的度数,再用直角三角形的面积减去扇形DOF的面积即可确定出阴影部分的面积.
,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,进而求出圆心角的度数,再用直角三角形的面积减去扇形DOF的面积即可确定出阴影部分的面积.
解:(1)![]() 与
与![]() 相切
相切
证明:连接![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]()
![]() ,
,![]() ,则
,则![]()
![]() ,
,![]() ,即
,即![]()
又 ![]() 过半径
过半径![]() 的外端点
的外端点![]() 与
与![]() 相切
相切

(2)设![]() ,则
,则![]() ,
,
根据勾股定理得 ![]() ,即
,即![]()
解得:![]() ,即
,即![]()
![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() 扇形
扇形![]() ,
,![]() 阴
阴![]() 扇形
扇形![]()
阴影部分的面积为![]() .
.

练习册系列答案
相关题目