Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖy=![]()
![]() x+8”Žx÷ŠĹĽ”ŕAĶ„£¨”Žy÷ŠĹĽ”ŕĶ„B£¨∂ĮĶ„Pī”AĶ„≥Ų∑Ę£¨“‘√Ņ√Ž2łŲĶ•őĽňŔ∂»—ō…šŌŖAO‘»ňŔ‘ň∂Į£¨Õ¨ Ī∂ĮĶ„Qī”BĶ„≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»—ō…šŌŖBA∑ĹŌÚŌÚĶ„A‘»ňŔ‘ň∂Į£¨ĶĪ“ĽłŲĶ„Õ£÷Ļ‘ň∂Į£¨ŃŪ“ĽłŲĶ„“≤ňś÷ģÕ£÷Ļ‘ň∂Į£¨Ń¨Ĺ”PQ£¨…Ť‘ň∂ĮĶń Īľšő™t£®√Ž£©£ģ
x+8”Žx÷ŠĹĽ”ŕAĶ„£¨”Žy÷ŠĹĽ”ŕĶ„B£¨∂ĮĶ„Pī”AĶ„≥Ų∑Ę£¨“‘√Ņ√Ž2łŲĶ•őĽňŔ∂»—ō…šŌŖAO‘»ňŔ‘ň∂Į£¨Õ¨ Ī∂ĮĶ„Qī”BĶ„≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»—ō…šŌŖBA∑ĹŌÚŌÚĶ„A‘»ňŔ‘ň∂Į£¨ĶĪ“ĽłŲĶ„Õ£÷Ļ‘ň∂Į£¨ŃŪ“ĽłŲĶ„“≤ňś÷ģÕ£÷Ļ‘ň∂Į£¨Ń¨Ĺ”PQ£¨…Ť‘ň∂ĮĶń Īľšő™t£®√Ž£©£ģ
£®1£©”√tĶńīķ ż ĹĪŪ ĺAP= £¨AQ=
£®2£©ĶĪtő™ļő÷Ķ Ī£¨PQ°őOB£Ņ
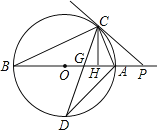
£®3£©»ŰĶ„Cő™∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶńŕ“ĽĶ„£¨ «∑Ůīś‘ŕt÷Ķ£¨ ĻĶ√“‘A°ĘP°ĘQ°ĘCő™∂•Ķ„ĶńňńĪŖ–őő™Ń‚–ő£Ņ»Űīś‘ŕ£¨«ů≥ŲQĶ„◊ÝĪÍ£¨»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ

°ĺīūįł°Ņ£®1£©![]() £¨
£¨![]() £Ľ£®2£©
£Ľ£®2£©![]() £Ľ£®3£©Ķ„
£Ľ£®3£©Ķ„![]() Ķń◊ÝĪÍő™
Ķń◊ÝĪÍő™![]() £¨
£¨![]() £¨
£¨![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›Ő‚“‚£¨Ō»«ů≥ŲĶ„AļÕĶ„BĶń◊ÝĪÍ£¨Ķ√ĶĹABĶń≥§∂»£¨łý囬∑≥Ő=ňŔ∂»![]() Īľš£¨ľīŅ…ĪŪ ĺ≥ŲAPļÕBQ£Ľ
Īľš£¨ľīŅ…ĪŪ ĺ≥ŲAPļÕBQ£Ľ
£®2£©”…£®1£©Ņ…÷™APļÕAQ£¨»ĽļůņŻ”√∆Ĺ––ŌŖ∑÷ŌŖ∂ő≥…Ī»ņż£¨ľīŅ…«ů≥ŲtĶń÷Ķ£Ľ
£®3£©∑÷»ż÷÷«ť–őŃ–≥Ų∑Ĺ≥Ő«ůĹ‚£ļĘŔĶĪ![]() £¨◊ų
£¨◊ų![]() £¨
£¨![]() £¨Ņ…Ķ√Ń‚–ő
£¨Ņ…Ķ√Ń‚–ő![]() £ĽĘŕĶĪ
£ĽĘŕĶĪ![]() Ī£¨◊ų
Ī£¨◊ų![]() £¨
£¨![]() £¨Ņ…Ķ√Ń‚–ő
£¨Ņ…Ķ√Ń‚–ő![]() £ĽĘŘĶĪ
£ĽĘŘĶĪ![]() Ī£¨◊ų
Ī£¨◊ų![]() £¨
£¨![]() £¨Ņ…Ķ√Ń‚–ő
£¨Ņ…Ķ√Ń‚–ő![]() £Ľ∑÷Īū«ů≥ŲĶ„QĶń◊ÝĪÍľīŅ….
£Ľ∑÷Īū«ů≥ŲĶ„QĶń◊ÝĪÍľīŅ….
Ĺ‚£ļ£®1£©łýĺ›Ő‚“‚£¨ŃÓ![]() £¨‘Ú
£¨‘Ú![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £Ľ
£Ľ
ŃÓ![]() Ī£¨
Ī£¨![]() £¨
£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗĶ„![]() £¨
£¨![]() £Ľ
£Ľ
‘ŕ![]() ÷–£¨”…ĻīĻ…∂®ņŪĶ√£¨
÷–£¨”…ĻīĻ…∂®ņŪĶ√£¨![]() £¨
£¨
°ŖĶ„![]() ĶńňŔ∂» «√Ņ√Ž2łŲĶ•őĽ£¨Ķ„
ĶńňŔ∂» «√Ņ√Ž2łŲĶ•őĽ£¨Ķ„![]() ĶńňŔ∂» «√Ņ√Ž1łŲĶ•őĽ£¨
ĶńňŔ∂» «√Ņ√Ž1łŲĶ•őĽ£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
Ļ īūįłő™£ļ![]() £¨
£¨![]() £Ľ
£Ľ
£®2£©»Ű![]() £¨»ÁÕľ£ļ
£¨»ÁÕľ£ļ
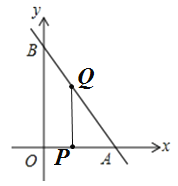
°ŗ![]() £¨
£¨
°Ŗ![]() £¨
£¨
°ŗ![]() £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ![]() £Ľ
£Ľ
£®3£©ĘŔ»ÁÕľ÷–£¨ĶĪ![]() £¨◊ų
£¨◊ų![]() £¨
£¨![]() £¨Ņ…Ķ√Ń‚–ő
£¨Ņ…Ķ√Ń‚–ő![]() £ģ
£ģ
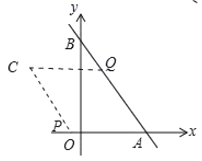
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £ģ
£ģ
…ŤĶ„Qő™£®![]() £¨
£¨![]() £©£¨
£©£¨
°ŗ![]() £¨
£¨
Ĺ‚Ķ√£ļ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗīň Ī![]() £Ľ
£Ľ
Ęŕ»ÁÕľ÷–£¨ĶĪ![]() Ī£¨◊ų
Ī£¨◊ų![]() £¨
£¨![]() £¨Ņ…Ķ√Ń‚–ő
£¨Ņ…Ķ√Ń‚–ő![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() ĹĽ
ĹĽ![]() ”ŕ
”ŕ![]() £ģ
£ģ
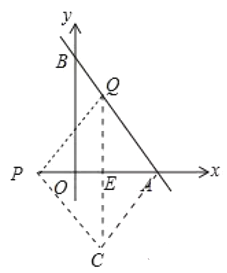
°ŖňńĪŖ–ő![]() «Ń‚–ő£¨
«Ń‚–ő£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £ģ
£ģ
”ŽĘŔÕ¨ņŪŅ…«ůĶ„QĶń◊ÝĪÍ£¨
°ŗīň Ī![]() £ģ
£ģ
ĘŘ»ÁÕľ÷–£¨ĶĪ![]() Ī£¨◊ų
Ī£¨◊ų![]() £¨
£¨![]() £¨Ņ…Ķ√Ń‚–ő
£¨Ņ…Ķ√Ń‚–ő![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() ĹĽ
ĹĽ![]() ”ŕ
”ŕ![]() £ģ
£ģ
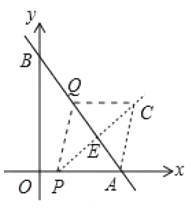
°ŖňńĪŖ–ő![]() «Ń‚–ő£¨
«Ń‚–ő£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ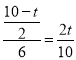 £¨
£¨
°ŗ![]() £ģ
£ģ
”ŽĘŔÕ¨ņŪŅ…«ůĶ„QĶń◊ÝĪÍ£¨
°ŗīň Ī![]() £ģ
£ģ
◊Ř…Ōňý Ų£¨¬ķ◊„ŐűľĢĶńĶ„![]() Ķń◊ÝĪÍő™£ļ
Ķń◊ÝĪÍő™£ļ![]() £¨
£¨![]() £¨
£¨![]() £ģ
£ģ

 √Ż ¶Ķ„ĺ¶◊÷ī ĺš∂ő∆™ŌĶŃ–īūįł
√Ż ¶Ķ„ĺ¶◊÷ī ĺš∂ő∆™ŌĶŃ–īūįł