Question

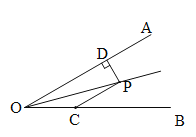
【题目】如图，点P是∠AOB的角平分线上一点，过P作PC//OA交OB于点C．若∠AOB＝30°，OC=4cm，则点P到OA的距离PD等于___________cm．

Answer 1

【答案】2

【解析】

过P作PM⊥OB于M，推出PD＝PM，根据角平分线定义和平行线性质求出∠POC＝∠CPO，推出OC＝PC＝4，求出∠PCM＝30°，求出PM即可．

过P作PM⊥OB于M．

∵OP平分∠AOB，∠AOB＝30°，∴∠AOP＝∠BOP=15°．

∵PC∥OA，∴∠AOP＝∠CPO，∠PCB＝∠AOB＝30°，∴∠POC＝∠CPO，∴PC＝OC＝4．

∵∠PCM＝30°，∴PMPC＝2．

∵OP平分∠AOB，PD⊥OA，PM⊥OB，∴PD＝PM＝2．

故答案为：2．