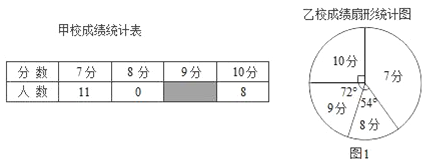
题目内容
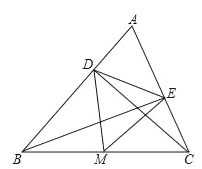
【题目】已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.
(1) 若DE=3,BC=8,求△DME的周长;
(2) 若∠A=60°,求证:∠DME=60°;
(3) 若BC2=2DE2,求∠A的度数.
【答案】(1)11;(2)见解析(3)∠A=45°
【解析】
试题(1)由三角形的高可以得到∠CDB=∠BEC=90°,再由直角三角形的斜边上的中点得出DM和EM的长,从而得结果.
(2)由直角三角形的斜边上的中点得出DM和EM的长,从而得DM=BM,EM=CM,进而得到∠DME=60°,
(3)由DM=EM=![]() BC,
BC,![]() 得
得![]() ,得到△DEM,从而求出结果.
,得到△DEM,从而求出结果.
试题解析:(1)∵∠CDB=∠BEC=90°,点M为BC的中点,
∴DM=EM=![]() BC=4,
BC=4,
又∵DE=3,
∴△DME的周长=DM+EM+DE=11;
(2)∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵DM=EM=![]() BC,
BC,
∴DM=BM,EM=CM,
∴∠DMB=180°-2∠ABC,∠EMC=180°-2∠ACB,
∴∠DME=180°-∠DMB-∠EMC=2(∠ABC+∠ACB)-180°,
∴∠DME=60°;
(3)∵DM=EM=![]() BC,BC2=2DE2,
BC,BC2=2DE2,
∴DM2=EM2=![]() DE2,
DE2,
∴![]() ,
,
∴∠DME=90°,
∴∠DMB+∠EMC=90°,
∵∠DMB=180°-2∠ABC,∠EMC=180°-2∠ACB,
∴∠ABC+∠ACB=135°,
∴∠A=45°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目