题目内容
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+4a﹣3(a≠0)的顶点为A. 
(1)求顶点A的坐标;
(2)过点(0,5)且平行于x轴的直线l,与抛物线y=ax2﹣4ax+4a﹣3(a≠0)交于B,C两点. ①当a=2时,求线段BC的长;
②当线段BC的长不小于6时,直接写出a的取值范围.
【答案】
(1)解:∵y=ax2﹣4ax+4a﹣3=a(x﹣2)2﹣3,
∴顶点A的坐标为(2,﹣3)
(2)解:①当a=2时,抛物线为y=2x2﹣8x+5,如图.
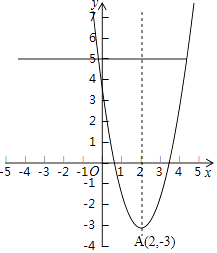
令y=5,得
2x2﹣8x+5=5,
解得,x1=0,x2=4,
∴ ![]() 线段BC的长为4,
线段BC的长为4,
②令y=5,得ax2﹣4ax+4a﹣3=5,
解得,x1= ![]() ,x2=
,x2= ![]() ,
,
∴线段BC的长为 ![]() ,
,
∵线段BC的长不小于6,
∴ ![]() ≥6,
≥6,
∴0<a≤ ![]() .
.
【解析】(1.)配方得到y=ax2﹣4ax+4a﹣3=a(x﹣2)2﹣3,于是得到结论; (2.)①当a=2时,抛物线为y=2x2﹣8x+5,如图.令y=5得到2x2﹣8x+5=5,解方程即可得到结论;②令y=5得到ax2﹣4ax+4a﹣3=5,解方程即可得到结论.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
相关题目