题目内容
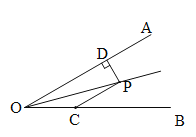
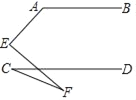
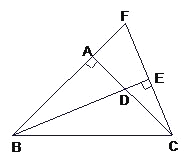
【题目】如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.
【答案】见解析。
【解析】
求出∠FBE=∠CBE,∠BEF=∠BEC=90°,根据ASA可证明Rt△BEF≌Rt△BEC,即可得CF=2CE,由等腰直角三角形的性质可得∠ABC=∠ACB=45°,根据BD是∠ABC的平分线可得∠F=∠ADB=67.5°,通过AAS可证明△ABD≌△ACF,根据全等三角形性质可得BD=CF,即可证明BD=2CE.
∵BD是∠ABC的平分线,
∴∠FBE=∠CBE,
∵BE⊥CF,
∴∠BEF=∠BEC=90°,
在Rt△BEF和Rt△BEC中,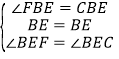 ,
,
∴Rt△BEF≌Rt△BEC(ASA).
∴CE=EF,
∴CF=2CE,
∵∠BAC=90°,且AB=AC,
∴∠FAC=∠BAC=90°,∠ABC=∠ACB=45°,
∵BD是∠ABC的平分线,
∴∠FBE=∠CBE=22.5°,
∴∠F=90°-22.5°=67.5°,∠ADB=90°-22.5°=67.5°,
∴∠F=∠ADB,
在△ABD和△ACF中,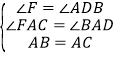 ,
,
∴△ABD≌△ACF(AAS),
∴BD=CF,
∵CF=2CE,
∴BD=2CE.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目