题目内容
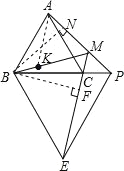
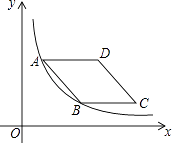
【题目】如图,已知等边△ABC 和等边△BPE,点 P 在 BC 的延长线上,EC 的延长线交 AP 于点 M,连接 BM;下列结论:①AP=CE;②∠PME=60°;③BM 平分∠AME;④AM+MC=BM,其中正确的有____________________(填序号).
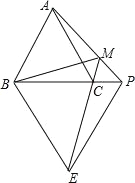
【答案】①②③④
【解析】
分别利用全等三角形的判定方法以及其性质得出对应角以及对应边关系进而分别分析得出答案.
证明:①∵等边△ABC 和等边△BPE,
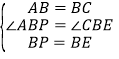 ∴AB=BC,∠ABC=∠PBE=60°,BP=BE, 在△APB 和△CEB 中
∴AB=BC,∠ABC=∠PBE=60°,BP=BE, 在△APB 和△CEB 中
∴△APB≌△CEB (SAS),
∴AP=CE,故此选项正确;
②∵△APB≌△CEB,
∴∠APB=∠CEB,
∵∠MCP=∠BCE,
则∠PME=∠PBE=60°,故此选项正确;
③作 BN⊥AM 于 N, BF⊥ME 于 F,
∵△APB≌△CEB,
∴∠BPN=∠FEB,
在△BNP 和△BFE 中,
∵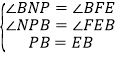
∴△BNP≌△BFE(AAS),
∴BN=BF,
∴BM 平分∠AME,故此选项正确;
④在 BM 上截取 BK=CM,连接 AK. 由②知∠PME=60°,
∴∠AMC=120°
由③知:BM 平分∠AME
∴∠BMC=∠AMK=60°
∴∠ABK+∠PBM=60°=∠PBM+∠ACM
∴∠ACM=∠ABK,
在△ABK 和△ACM 中
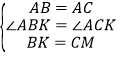
∴△ACM≌△ABK(SAS),
∴AK=AM,
∴△AMK 为等边三角形,则 AM=MK, 故 AM+MC=BM,故此选项正确;故答案为:①②③④.
|

练习册系列答案
相关题目