题目内容
【题目】如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC。
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC。

【答案】(1)证明见解析;(2)50°
【解析】
(1)首先连接AC,根据AM⊥CD,AN⊥BC,判断出AM、AN分别是CD、BC的垂直平分线,得到AC=AD,AB=AC,再根据等腰三角形三线合一的性质得到∠DAM=∠CAM,∠BAN=∠CAN,然后根据角的和差即可得出结论;
(2)由∠MAN=70°,得出∠BAD的度数.由四边形ANCM内角和等于360°,得到∠BCD的度数.在△BCD中,由三角形内角和定理得到∠BDC的度数.在△ABD中,根据等腰三角形的性质和三角形内角和定理可得出∠ADB的度数,根据角的和差即可得出结论.
(1)如图,连接AC.
∵M、N分别是CD、BC的中点,且AM⊥CD,AN⊥BC,∴AM、AN分别是CD、BC的垂直平分线,∴AC=AD,AB=AC.
∵AM⊥CD,AN⊥BC,∴∠DAM=∠CAM,∠BAN=∠CAN,∴∠DAC+∠BAC=2∠CAM+2∠CAN,∴∠BAD=2∠MAN;
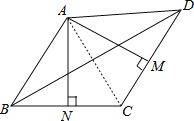
(2)∵∠MAN=70°,∴∠BAD=2∠MAN=140°.
∵AM⊥CD,AN⊥BC,∴∠BCD=180°-∠MAN=180°-70°=110°.
∵∠DBC=40°,∴∠BDC=180°-∠DBC-∠BCD=180°-40°-110°=30°.
∵AB=AC=AD,∴∠ABD=∠ADB.
∵∠BAD=140°,∴∠ABD=∠ADB=20°,∴∠ADC=∠ADB+∠BDC=20°+30°=50°.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目