题目内容
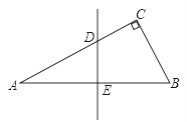
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是________
【答案】(1)(2)(3)
【解析】根据线段垂直平分线的性质和等腰三角形ABC的顶角为36°,求出各角的度数,然后对各选项分析判断后利用排除法求解.
解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵DE是AB的垂直平分线,
∴AD=BD,∠ABD=∠A=36°,
∴∠DBC=72°-36°=36°,
∠BDC=180°-36°-72°=72°,
∴BD=BC;
(1)BD平分∠ABC正确;
(2)AD=BD=CD正确;
(3)△BDC的周长=BC+CD+BD
=BC+CD+AD
=BC+AC
=AB+BC,正确;
(4)AD=BD≠CD,所以D不是AC的中点,故本选项错误.
故正确的命题是(1)(2)(3).
主要考查线段垂直平分线上的点到线段两端点的距离相等的性质和特殊等腰三角形“黄金三角形”的性质,需要熟练掌握并灵活运用,求得各角得度数是正确解答本题的关键.

练习册系列答案
相关题目
【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整). 
分数(分) | 人数(人) |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?