题目内容
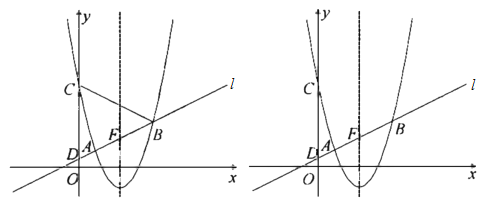
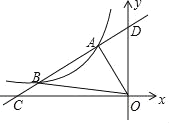
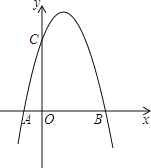
【题目】如图已知在直角坐标系中，一条抛物线与x轴交于A、B两点，与y轴交于C点，其中B（3，0），C（0，4），点A在x轴的负半轴上，OC＝4OA．
（1）求点A坐标；
（2）求这条抛物线的解析式，并求出它的顶点坐标．
【答案】（1）点A的坐标为（﹣1，0）；（2）y＝
+4，顶点坐标是（1，
）．
【解析】
（1）根据B（3，0），C（0，4），点A在x轴的负半轴上，OC＝4OA，可以求得OA的长，从而可以得到点A的坐标；
（2）根据点A和点B的坐标可以设出该抛物线的解析式，然后根据抛物线经过点C可以求得该抛物线的解析式，再将解析式化成顶点式可得抛物线的顶点坐标．
解：（1）∵B（3，0），C（0，4），点A在x轴的负半轴上，OC＝4OA，
∴OC＝4，
∴OA＝1，
∴点A的坐标为（﹣1，0）；
（2）设这条抛物线的解析式为y＝a（x+1）（x﹣3），
∵点C（0，4）在此抛物线上，
∴4＝a（0+1）（0﹣3），
解得，a＝﹣
，
∴y＝﹣（x+1）（x﹣3）＝+4＝﹣
，
∴该抛物线的顶点坐标为（1，），
即这条抛物线的解析式为y＝+4，它的顶点坐标是（1，）．
练习册系列答案
相关题目
