ЬтФПФкШн
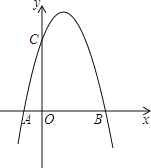
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНЉ![]() x2+bx+cгыxжсНЛгкBЁЂCСНЕуЃЈЕуBдкЕуCЕФзѓВрЃЉЃЌгыyжсНЛгкЕуAЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌBЃЈЉ3ЃЌ0ЃЉЃЌAЃЈ0ЃЌ
x2+bx+cгыxжсНЛгкBЁЂCСНЕуЃЈЕуBдкЕуCЕФзѓВрЃЉЃЌгыyжсНЛгкЕуAЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌBЃЈЉ3ЃЌ0ЃЉЃЌAЃЈ0ЃЌ![]() ЃЉ
ЃЉ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНМАDЕузјБъЃЛ
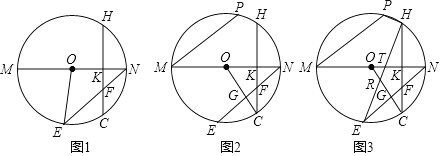
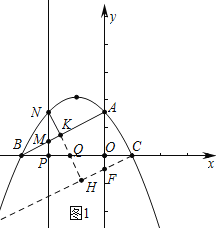
ЃЈ2ЃЉШчЭМ1ЃЌPЮЊЯпЖЮOBЩЯЃЈВЛгыOЁЂBжиЩсЃЉвЛЖЏЕуЃЌЙ§ЕуPзїyжсЕФЦНааЯпНЛЯпЖЮABгкЕуMЃЌНЛХзЮяЯпгкЕуNЃЌЕуNзїNKЁЭBAНЛBAгкЕуKЃЌЕБЁїMNKгыЁїMPBЕФУцЛ§ЯрЕШЪБЃЌдкXжсЩЯеввЛЖЏЕуQЃЌЪЙЕУ![]() CQ+QNзюаЁЪБЃЌЧѓЕуQЕФзјБъМА
CQ+QNзюаЁЪБЃЌЧѓЕуQЕФзјБъМА![]() CQ+QNзюаЁжЕЃЛ
CQ+QNзюаЁжЕЃЛ
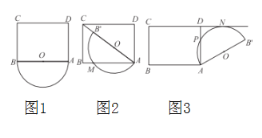
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЁїODNбиЩфЯпDNЦНвЦЃЌЦНвЦКѓЕФЖдгІШ§НЧаЮЮЊЁїOЁфDЁфNЁфЃЌНЋЁїAOCШЦЕуOФцЪБеыа§зЊЕНA1OC1ЕФЮЛжУЃЌЧвЕуC1ЧЁКУТфдкACЩЯЃЌЁїA1DЁфNЁфЪЧЗёФмЮЊЕШбќШ§НЧаЮЃЌШєФмЧѓГіNЁфЕФзјБъЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
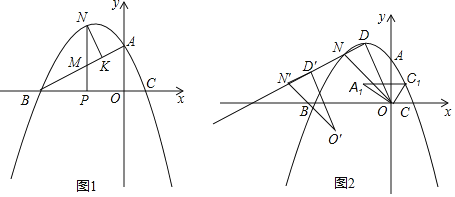
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2Љ
x2Љ![]() x+
x+![]() ЃЛЖЅЕуDЕФзјБъЮЊЃЈЉ1ЃЌ
ЃЛЖЅЕуDЕФзјБъЮЊЃЈЉ1ЃЌ![]()
![]() ЃЉЃЛЃЈ2ЃЉQЃЈЉ1ЃЌ0ЃЉЃЌзюаЁжЕЮЊ3ЃЛЃЈ3ЃЉNЁфЕФзјБъЮЊЃЈЉ
ЃЉЃЛЃЈ2ЃЉQЃЈЉ1ЃЌ0ЃЉЃЌзюаЁжЕЮЊ3ЃЛЃЈ3ЃЉNЁфЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈвдМАЖЅЕузјБъЙЋЪНМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉШчЭМ1жаЃЌЩшPЃЈmЃЌ0ЃЉдђNЃЈmЃЌЉ![]() m2Љ
m2Љ![]() m+
m+![]() ЃЉЃЎгЩЁїNMKЁзЁїBMNЃЌгжЁїMNKгыЁїMPBЕФУцЛ§ЯрЕШЃЌЭЦГіЁїNMKЁеЁїBMNЃЌЭЦГіMNЃНBMЃЌдкRtЁїABOжаЃЌtanЁЯABOЃН
ЃЉЃЎгЩЁїNMKЁзЁїBMNЃЌгжЁїMNKгыЁїMPBЕФУцЛ§ЯрЕШЃЌЭЦГіЁїNMKЁеЁїBMNЃЌЭЦГіMNЃНBMЃЌдкRtЁїABOжаЃЌtanЁЯABOЃН![]() ЃН
ЃН![]() ЃЌЭЦГіЁЯABOЃН30ЁуЃЌЭЦГіBMЃН2PMЃНMNЃЌПЩЕУЉ
ЃЌЭЦГіЁЯABOЃН30ЁуЃЌЭЦГіBMЃН2PMЃНMNЃЌПЩЕУЉ![]() m2Љ
m2Љ![]() m+
m+![]() Љ
Љ![]() m+
m+![]() ЃН2ЃЈ
ЃН2ЃЈ![]() m+
m+![]() ЃЉЃЌНтЕУmЃНЉ2ЛђЉ3ЃЈЩсЦњЃЉЃЌЭЦГіNЃЈЉ2ЃЌ
ЃЉЃЌНтЕУmЃНЉ2ЛђЉ3ЃЈЩсЦњЃЉЃЌЭЦГіNЃЈЉ2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
дкyжсЩЯШЁвЛЕуFЃЌЪЙЕУЁЯOCFЃН30ЁуЃЌзїQHЁЭCFгкHЃЌвђЮЊQHЃН![]() CQЃЌЫљвдNQ+
CQЃЌЫљвдNQ+![]() CQЃНNQ+QHЃЌИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБNЁЂQЁЂHЙВЯпЃЌЧвNHЁЭCFЪБЃЌNQ+
CQЃНNQ+QHЃЌИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБNЁЂQЁЂHЙВЯпЃЌЧвNHЁЭCFЪБЃЌNQ+![]() CQЃНNQ+QHЕФжЕзюаЁЃЎгЩДЫМДПЩНтОіЮЪЬтЃЎ
CQЃНNQ+QHЕФжЕзюаЁЃЎгЩДЫМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЪзЯШЧѓГіЕуAЁфЕФзјБъЃЌдйжЄУїAЁфNЁЭDNЃЌЗжШ§жжЧщаЮЬжТлМДПЩЃЎЂйШчЭМ3жаЃЌЕБAЁфDЁфЃНAЁфNЁфЪБЃЎЂкШчЭМ4жаЃЌЕБNЁфDЁфЃНNЁфAЁфЪБЃЎЂлШчЭМ5жаЃЌбгГЄCЁфAЁфНЛDGгкNЁфЃЌДЫЪБЁїDЁфNЁфAЁфЪЧЕШбќШ§НЧаЮЃЎ
НтЃКЃЈ1ЃЉАбBЃЈЉ3ЃЌ0ЃЉЃЌAЃЈ0ЃЌ![]() ЃЉЕФзјБъДњШыyЃНЉ
ЃЉЕФзјБъДњШыyЃНЉ![]() x2+bx+cЃЌЕУЕН
x2+bx+cЃЌЕУЕН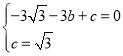 ЃЌ
ЃЌ
НтЕУ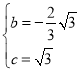 ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊyЃНЉ![]() x2Љ
x2Љ![]() x+
x+![]() ЃЌ
ЃЌ
ЖЅЕуDЕФзјБъЮЊЃЈЉ1ЃЌ![]()
![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ2ЃЉШчЭМ1жаЃЌЩшPЃЈmЃЌ0ЃЉдђNЃЈmЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпAЃЈ0ЃЌ![]() ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉЃЌ
ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊyЃН![]() x+
x+![]() ЃЌABгУPNЕФНЛЕуMЃЈmЃЌ
ЃЌABгУPNЕФНЛЕуMЃЈmЃЌ![]() m+
m+![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЁЯNMKЃНЁЯBMPЃЌЁЯNKMЃНЁЯMPBЃН90ЁуЃЌ
ЁрЁїNMKЁзЁїBMNЃЌ
ЁпЁїMNKгыЁїMPBЕФУцЛ§ЯрЕШЃЌ
ЁрЁїNMKЁеЁїBMNЃЌ
ЁрMNЃНBMЃЌ
дкRtЁїABOжаЃЌtanЁЯABOЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЁЯABOЃН30ЁуЃЌ
ЁрBMЃН2PMЃНMNЃЌ
ЁрЉ![]() m2Љ
m2Љ![]()
![]() m+
m+![]() Љ
Љ![]() m+
m+![]() ЃН2ЃЈ
ЃН2ЃЈ![]() m+
m+![]() ЃЉЃЌ
ЃЉЃЌ
НтЕУmЃНЉ2ЛђЉ3ЃЈЩсЦњЃЉЃЌ
ЁрNЃЈЉ2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
дкyжсЩЯШЁвЛЕуFЃЌЪЙЕУЁЯOCFЃН30ЁуЃЌзїQHЁЭCFгкHЃЌ
ЁпQHЃН![]() CQЃЌ
CQЃЌ
ЁрNQ+![]() CQЃНNQ+QHЃЌ
CQЃНNQ+QHЃЌ
ИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБNЁЂQЁЂHЙВЯпЃЌЧвNHЁЭCFЪБЃЌNQ+![]() CQЃНNQ+QHЕФжЕзюаЁЃЎ
CQЃНNQ+QHЕФжЕзюаЁЃЎ
ЁпжБЯпCFЕФНтЮіЪНЮЊyЃН![]() xЉ
xЉ![]() ЃЌжБЯпNHЕФНтЮіЪНЮЊyЃНЉ
ЃЌжБЯпNHЕФНтЮіЪНЮЊyЃНЉ![]() xЉ
xЉ![]() ЃЌ
ЃЌ
ЁрQЃЈЉ1ЃЌ0ЃЉЃЌ
гЩ ЃЌНтЕУ
ЃЌНтЕУ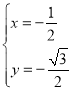 ЃЌ
ЃЌ
ЁрHЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрNHЃН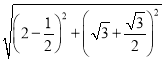 ЃН3ЃЌ
ЃН3ЃЌ
ЁрNQ+![]() CQЃНNQ+QHЕФзюаЁжЕЮЊ3ЃЎ
CQЃНNQ+QHЕФзюаЁжЕЮЊ3ЃЎ
ЃЈ3ЃЉШчЭМ2жаЃЌ
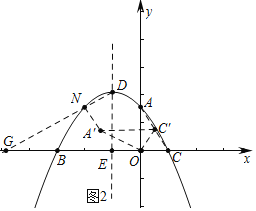
дкRtЁїAOCжаЃЌЁпOAЃН![]() ЃЌOCЃН1ЃЌACЃН2ЃЌ
ЃЌOCЃН1ЃЌACЃН2ЃЌ
ЁрtanЁЯACOЃН![]() ЃЌ
ЃЌ
ЁрЁЯACOЃН60ЁуЃЌ
ЁпOCЁфЃНOCЃЌ
ЁрЁїCOCЁфЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯAЁфCЁфCЃНЁЯCЁфOCЃН60ЁуЃЌ
ЁрAЁфCЁфЁЮOCЃЌ
ЁрAЁфЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпNЃЈЉ2ЃЌ![]() ЃЉЃЌDЃЈЉ1ЃЌ
ЃЉЃЌDЃЈЉ1ЃЌ![]()
![]() ЃЉЃЌ
ЃЉЃЌ
ЁржБЯпDNЕФНтЮіЪНЮЊyЃН![]() x+
x+![]()
![]() ЃЌжБЯпAЁфNЕФНтЮіЪНyЃНЉ
ЃЌжБЯпAЁфNЕФНтЮіЪНyЃНЉ![]() xЉ
xЉ![]() ЃЌ
ЃЌ
Ёп![]() ЁСЃЈЉ
ЁСЃЈЉ![]() ЃЉЃНЉ1ЃЌ
ЃЉЃНЉ1ЃЌ
ЁрANЁЭDNЃЌЩшжБЯпDNНЛxжсгкGЃЌдђGЃЈЉ5ЃЌ0ЃЉЃЌЖдГЦжсгыxжсЕФНЛЕуЮЊEЃЈЉ1ЃЌ0ЃЉЃЌ
дкRtЁїDGEжаЃЌtanЁЯDGEЃН![]() ЃЌ
ЃЌ
ЁрЁЯDGEЃН30ЁуЃЎ
ЂйШчЭМ3жаЃЌЕБAЁфDЁфЃНAЁфNЁфЪБЃЌвзжЊNDЁфЃНNNЁфЃЌAЁфNЃН1ЃЌNDЁфЃНNNЁфЃН![]() ЃЌвзжЄЁїAЁфNЁфDЁфЪЧЕШБпШ§НЧаЮЃЌПЩЕУNЁфЃЈЉ
ЃЌвзжЄЁїAЁфNЁфDЁфЪЧЕШБпШ§НЧаЮЃЌПЩЕУNЁфЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
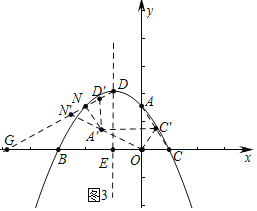
ЂкШчЭМ4жаЃЌЕБNЁфDЁфЃНNЁфAЁфЪБЃЌЁпAЁфNЃН1ЃЌDNЃН![]() ЃЌ
ЃЌ
дкRtЁїAЁфNЁфNжаЃЌAЁфNЁфЃНNЁфDЁфЃН![]() ЃЌAЁфNЃН1ЃЌNNЁфЃН
ЃЌAЁфNЃН1ЃЌNNЁфЃН![]() ЃЌвзжЄЁїAЁфNЁфDЁфЪЧЕШБпШ§НЧаЮЃЌ
ЃЌвзжЄЁїAЁфNЁфDЁфЪЧЕШБпШ§НЧаЮЃЌ
ЁрNЁфЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
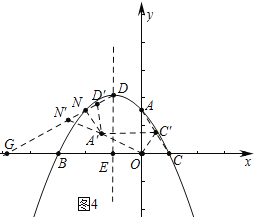
ЂлШчЭМ5жаЃЌбгГЄCЁфAЁфНЛDGгкNЁфЃЌДЫЪБЁїDЁфNЁфAЁфЪЧЕШбќШ§НЧаЮЃЎ
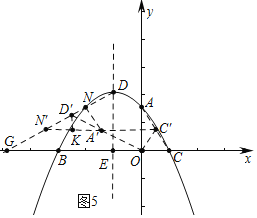
РэгЩЃКзїDЁфKЁЭCЁфNЁфгкKЃЌвзжЊNЁфЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрAЁфNЁфЃН2ЃЌ
дкRtЁїDЁфNЁфKжаЃЌЁпЁЯDЁфNЁфKЃН30ЁуЃЌDЁфNЁфЃН![]() ЃЌ
ЃЌ
ЁрDЁфKЃН![]() ЃЌKNЁфЃН1ЃЌ
ЃЌKNЁфЃН1ЃЌ
ЁрKAЁфЃНAЁфNЁфЉNЁфKЃН2Љ1ЃН1ЃЌ
дкRtЁїAЁфDЁфKжаЃЌAЁфDЁфЃН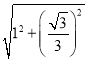 ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDЁфNЁфЃНDЁфAЁфЃЌ
ЁрЁїAЁфDЁфNЁфЪЧЕШбќШ§НЧаЮЃЌ
злЩЯЫљЪіЃЌЕБЕуNЁфЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЪБЃЌЁїAЁфDЁфNЁфЪЧЕШбќШ§НЧаЮЃЎ
ЃЉЪБЃЌЁїAЁфDЁфNЁфЪЧЕШбќШ§НЧаЮЃЎ

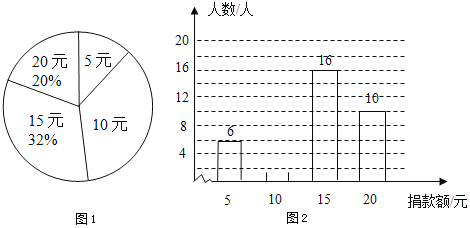
ЁОЬтФПЁПОрРыжаПМЬхПМЪБМфдНРДдННќЃЌФъМЖзщЯыСЫНтГѕШ§ФъМЖ2400УћбЇЩњжмФЉдкМвЬхг§ЖЭСЖЕФЧщПіЃЌдкГѕШ§ФъМЖЫцЛњГщВщСЫ20УћФаЩњКЭ20УћХЎЩњжмФЉУПЬьдкМвЖЭСЖЕФЪБМфЧщПіЃЎ
ЃЈвЛЃЉЪеМЏЪ§ОнЃКЃЈЕЅЮЛЃКЗжЃЉ
ФаЩњЃК20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40
ХЎЩњЃК75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90
ЃЈЖўЃЉећРэЁЂУшЪіЪ§ОнЃКЃЈБэвЛЃЉ
ЪБМфx | xЁм30 | 30ЃМxЁм60 | 60ЃМxЁм90 | 90ЃМxЁм120 |
ФаЩњ | 2 | 8 | 8 | 2 |
ХЎЩњ | 1 | 4 | a | 3 |
ЃЈБэЖўЃЉСНзщЪ§ОнЕФМЋВюЁЂЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§
МЋВю | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | |
ФаЩњ | 100 | 65.75 | b | c |
ХЎЩњ | 90 | 75.5 | 75 | 75 |
ЃЈШ§ЃЉЗжЮіЁЂгІгУЪ§ОнЃК
ЃЈ1ЃЉЧыНЋЩЯУцСНИіБэИёВЙГфЭъећЃКaЃН_____ЃЌbЃН______ЃЌcЃН______ЃЛ
ЃЈ2ЃЉЧыИљОнГщбљЕїВщЕФЪ§ОнЙРМЦГѕШ§ФъМЖжмФЉУПЬьЖЭСЖЪБМфдк100ЗжжгвдЩЯЃЈКЌ100ЗжжгЃЉЕФЭЌбЇДѓдМгаЖрЩйШЫЃП
ЃЈ3ЃЉРюРЯЪІПДСЫБэИёЪ§ОнКѓШЯЮЊГѕШ§ФъМЖЕФХЎЩњжмФЉЖЭСЖМсГжЕУБШФаЩњКУЃЌЧыФуНсКЯЭГМЦЪ§ОнЃЌаДГіжЇГжРЯЪІЙлЕуЕФРэгЩЃЎ