Question

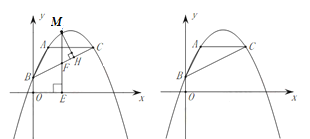
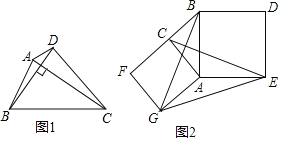
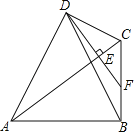
【题目】如图，四边形ABCD中，∠ADC＝∠ABC＝90°，连接AC、BD，作DF⊥AC，交AC于点E，交BC于点F，∠ADB＝2∠DBC，若BC＝，DF＝5，则AB的长为_____．

Answer 1

【答案】6．

【解析】

作辅助线，根据等腰三角形三线合一的性质得AG=BG，根据矩形的性质和判定证明DN=BG，设DN=a，则AB=2a，证明△FDN∽△ACB，列比例式可表示FN，由勾股定理可得结论．

如图，过D作DG⊥AB于G，DN⊥BC交BC的延长线于N，

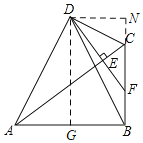
∵∠AGD=∠ABC=90°，

∴DG∥BC，

∴∠DBC=∠BDG，

∵∠ADB=2∠DBC，

∴∠ADG=∠BDG，

∵DG⊥AB，

∴AG=BG，

∵∠N=∠ABC=∠DGB=90°，

∴四边形DGBN是矩形，

∴DN=BG，

设DN=a，则AB=2a，

∵DF⊥AC，

∴∠FEC=∠ACB+∠CFE=90°，

∵∠ACB+∠CAB=90°，

∴∠CFE=∠CAB，

∵∠N=∠ABC=90°，

∴△FDN∽△ACB，

∴，即，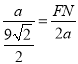

FN=，

Rt△DFN中，由勾股定理得：DF2=DN2+FN2，

∴，

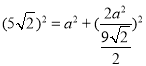设a2=b，

则50=b+，

8b2+81b﹣4050=0，

(b﹣18)(8b+225)=0，

b1=18，b2=﹣(舍)，

∴a2=18，

∵a＞0，

∴a=3，

∴AB=2a=6，

故答案为：6．