Question

【题目】已知矩形ABCD，E为CD的中点，F为AB上一点，连接EF，DF，若AB＝4，BC＝2，EF＝，则DF的长为_____．

Answer 1

【答案】或

【解析】

分两种情况：①点F靠近点A时，作FG⊥CD于G，则FG＝BC＝2，∠FGE＝90°，由勾股定理求出GE，由矩形的性质和已知条件得出DG，由勾股定理求出DF的长；

②点F靠近点B时，作FG⊥CD于G，则FG＝BC＝2，∠FGE＝90°，同①得出EG＝1，得出DG＝DE+EG＝3，由勾股定理求出DF的长即可．

解：分两种情况：

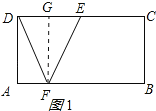
①点F靠近点A时，如图1所示：

作FG⊥CD于G，

则FG＝BC＝2，∠FGE＝90°，

∴GE＝＝＝1，

∵四边形ABCD是矩形，

∴CD＝AB＝4，AD＝BC＝2，

∵E是CD的中点，

∴DE＝CD＝2，

∴DG＝2﹣1＝1，

∴DF＝＝＝；

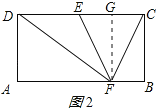
②点F靠近点B时，如图2所示：

作FG⊥CD于G，

则FG＝BC＝2，∠FGE＝90°，

同①得出EG＝1，

∴DG＝DE+EG＝3，

∴DF＝＝＝，

综上所述：DF的长为或．